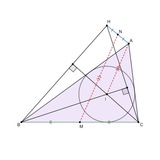
Отличие от случая инцентра в том, что инцентр всегда лежит внутри вписанной окружности, а вот точка P при P-сопряжении может быть как внутри, так и вне (да, да, на окружности тоже может быть). Если она внутри, то таких пар точек 3: пересечения прямых, образованных точками пересечения прямых B1C1 с AP, A1B1 с CP, A1C1 с BP, с вписанной окружностью. Если же P снаружи, то добавляется пара точек, являющихся пересечениями поляры P с вписанной окружностью, и сопряженных пар в итоге 4. Отсюда и получилась задача, которая была на финале ЮМТ.

А конструкция с картинки является леммой для доказательства утверждений про колличество пар P-сопряженных точек: зеленые прямые P-сопряжены для верхнего угла <=> пунктирные прямые проходят через синие точки, где синие прямые - это AP и дополняющая AB, AC, AP до гармонической четверки

Задача 76:

Пусть I - инцентр ABC, D - точка касания вписанной с BC, P - проекция I на сер пер к AD. Докажите, что углы BPI и CPI равны

Задача 77:

Дан треугольник ABC с прямым углом A и точка D на его катете AC. Пусть E - отражение A относительно BD. Точка F на CE такова, что DF перпендикулярно BC. Докажите, что прямые AF, DE и BC пересекаются в одной точке.

Задача 78:

Дан гармонический четырехугольник ABCD. Точка K на прямой AB такова, что угол BCK прямой. Прямая KD пересекает AC и (ABC) в точках N и E. H - основание высоты из A на BC, M - середина отрезка AC, F - середина дуги BAC. Оказалось, что четырехугольник BHMF - вписанный. Докажите, что BE = AN

Задача 79:

Парабола с фокусом F касается сторон АВ и АС треугольника АВС, она пересекает сторону ВС в точках M и N, а прямая АF пересекает ВС в точке W.доказать что окружности (МWF) и (NWF) касаются окружности (АВС)

Задача 80:

Сегодняшнее обсуждение в олгео напомнило вот такую задачу, думаю условие и из картинки всем понятно. А изначально в чате всплыл следующий факт:
Дана коника с фокусом F и касающаяся ее прямая l. Докажите, что проекция F на l лежит на фиксированной окружности, не зависящей от выбора l

Сегодня 1 декабря, а это значит, что начался заочный тур олимпиады имени И.Ф.Шарыгина!

На сайте уже появился вариант! По-моему он довольно хороший. Приятного времяпровождения!

Задача 81:

Не так давно благодаря кубку Колмогорова стал печально известен внешний случай леммы Саваямы, который, конечно, не верен, в чем легко убедиться простым советским построением в геогебре. По такому случаю предлагаю порешать внешний случай аватарки GeoCraft (формулировать я ее не буду, а то еще скажут, что неверно...)

Задача 82:

Дан треугольник ABC с инцентром I. Отличная от BC прямая, касающаяся его вписанной окружности и параллельная BC, пересекает (ABC) в точках X и Y. Докажите, что AX * AY = AI²

Задача 83:

Дан равнобедренный треугольник ABC с основанием BC. На (ABC) выбирается произвольная точка P. Серпер к AP пересекает AB и AC в точках X и Y.  M и N - середины AC и AB. Докажите, что прямые AP, MX и NY пересекаются в одной точке

Задача 84:

Дан треугольник ABC. Касательные в B и C к (ABC) пересекаются в T. Точки X и Y на BC таковы, что AX // BT и AY // CT. M и N - середины AB и AC. Докажите, что прямые MX, NY и AT пересекаются в одной точке

С новым годом!🎄