Задача 1:
Автор - GeoGen, Пучков Пётр

Дан треугольник ABC с инцентром I. H - ортоцентр треугольника BIC. M и N - середины отрезков BC и AH соответственно. Докажите, что прямые AI и MN параллельны.

Задача 2:
Автор - GeoGen, Ким Пётр

В треугольнике ABC вписанная окружность с центром в I касается стороны BC в точке D. Прямая ID вторично пересекает описанную окружность треугольника BIC в точке J. M - середина BC. G - середина MJ.
Докажите, что A, D, G лежат на одной прямой.

Задача 3:
Автор - GeoGen, Ким Пётр

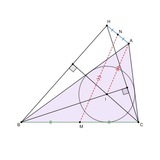
В треугольнике ABC вписанная окружность с центром в I касается стороны BC в точке D. Прямая ID вторично пересекает описанную окружность треугольника BIC в точке J. M - середина BC, L - проекция M на BJ. Прямая LD вторично пересекает описанную окружность треугольника ADC в точке K. Докажите, что AK = KD.

Задача 4:
Автор - GeoGen, Чуев Савва

Дан треугольник ABC с прямым углом A. I - его инцентр. На лучах BA и CA выбираются такие точки D и E соответственно, что DB = BC = CE. Докажите, что центр описанной окружности треугольника DIE лежит на описанной окружности треугольника ABC.

Задача 5:
Автор - GeoGen, Пучков Пëтр

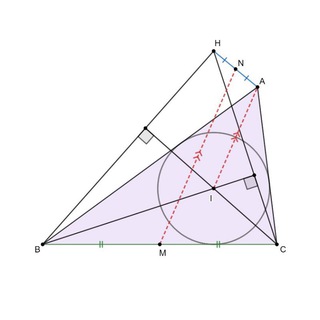
В треугольнике ABC H - ортоцентр, а E - основание биссектрисы угла BAC. I - центр вписанной окружности треугольника BHC. H' - симметрична H относительно E. Окружность (H'IH) пересекает AI в точках I и T.
Докажите, что точки H', E, T, A лежат на одной окружности

Задача 6:
Автор - GeoGen, Ким Пётр

В треугольнике ABC вписанная окружность с центром I касается стороны AC в точке D. Внешняя биссектриса угла A пересекает BD в точке E, а внешняя биссектриса угла C - в точке F. M - середина CI. FM пересекает BI в точке K.
Доказать, что окружности BCK и ADE касаются.

Задача 7:
Автор - GeoGen, Чуев Савва

Дан треугольник ABC с прямым углом A, I - его инцентр. Точки X и Y выбраны на лучах BA и CA соответственно так, что BX = CY = (BA + CA)/2. I' - точка, симметричная I относительно прямой BC, H - ортоцентр треугольника BIC. Под каким углом виден отрезок XY из точки M, если M - середина отрезка I'H?

Задача 8:
Автор - GeoGen, Ким Пётр

В треугольнике ABC вписанная окружность с центром в I касается AC в точке D. Прямая BD пересекает внешние биссектрисы углов A и С в точках E и F соответственно. F' - отражение F относительно С. IF' пересекает BD в точке G. Доказать, что описанные окружности треугольников FEF' и IDG касаются.