Задача 63:

На дугах AC и AB окружности (ABC) выбраны точки P и Q соответственно так, что PQ || AB. R и S - основания перпендикуляров из P и Q на AC и AB соответственно. Докажите, что R и S равноудалены от середины отрезка PQ

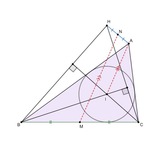
Задача 64:

Дан четырехугольник ABCD, описанный вокруг окружности с центром I. Пусть P - точка внутри ABCD такая, что периметры треугольников APB, BPC, CPD и DPA равны. На отрезках PA, PB, PC и PD откладываются на равное расстояние от P точки A', B', C' и D' соответственно. Докажите, что прямые A'C', B'D' и PI пересекаются в одной точке

Задача 65:
Авторы - Пучков Пëтр, GeoGen

В треугольнике ABC Ш_{BAC} - точка Шалтая для вершины A. D - проекция Ш_{BAC} на AC. Б_{ADB} - точка Болтая треугольника ADB для вершины D. Прямая AБ_{ADB} пересекает BC в точке E.
Докажите, что окружности (AШ_{BAC}C) и (BБ_{ADB}E) касаются

Задача 66:

В треугольнике ABC на стороне BC, как на основании, построены в обе стороны равнобедренные прямоугольные треугольники BPC и BQC. Прямые BP и BQ пересекают прямую AC в точках X и Y соответственно. Прямые CP и CQ пересекают прямую AB в точках Z и T соответственно. Докажите, что XZ // YT

Задача 67:
Автор — Ким Пётр

В треугольнике ABC на сторонах AB и AC выбраны точки D и E соответственно таким образом, что DE параллельно BC. Точка F на BC выбрана таким образом, что четырёхугольник ADFE — описанный.
Доказать, что (DEF) касается вписанной окружности треугольника ABC.

Задача 68:
Автор — Ким Пётр

Лучи l и m образуют угол, в который вписаны окружности a и b. Окружность c касается a внутренним образом, а b — внешним. Окружность d касается a внешним образом, а b — внутренним. Точки A,B,C,D — пересечения c с лучами l и m. Точки X,Y,Z,T — пересечения d с лучами l и m.
Докажите, что из набора (A,B,C,D) и из набора (X,Y,Z,T) можно выбрать по паре точек таким образом, что четырёхугольник (невырожденный), образованный ими будет (не обязательно одновременное выполнение обоих условий):
а) вписанным
б) описанным

Задача 69:

Пусть точки P и Q изогонально сопряжены в треугольнике ABC. Касательные к окружностям (BPC) и (BQC) в точках P и Q соответственно пересекаются в точке R. Докажите, что (ABC), (PQR) и AR имеют общую точку

Задача 70:

Четырехугольник ABCD описан вокруг окружности с центром I. Пары лучей BA, CD и AD, BC пересекаются в точках E и F соответственно. O_F и O_E - центры (ABF) и (CBE) соответственно. Докажите, что угол DIO_F прямой тогда и только тогда, когда угол DIO_E прямой

Задача 71:

Пусть AD, BE, CF - высоты остроугольного треугольника ABC. EF пересекает меньшие дуги AB и AC окружности (ABC) в точках X и Y соответственно. BX и BY пересекает DF в точках P и Q соответственно. CX и CY пересекает DE в точках R и S соответственно. Докажите, что точки P, Q, R, S, X, Y лежат на одной окружности

Задача 72: (авторка)

Пусть M - середина стороны BC треугольника ABC. X и Y - основания перпендикуляров из M на AC и AB соответственно. H_AXB и H_AYC - ортоцентры понятно каких треугольников. Докажите, что точки H_AXB, H_AYC, B, C лежат на одной окружности

Задача 73: [отбор в тг10] [[авторка]]

M - центр масс остроугольного треугольника ABC, а BP и CQ - его высоты. Лучи MP и MQ пересекают (ABC) в точках R и S. Оказалось, что AM = BC. Докажите, что прямая SR проходит через ортоцентр ABC

Задача 74: [ЮМТ2025] [[опять авторка >_<]]

В остроугольном неравнобедренном треугольнике ABC отметили точки Ib и Ic - центры вневписанных окружностей напротив вершин B и C соответственно. Пусть D - проекция точки A на прямую BC. Точка X - ортоцентр треугольника IbIcD. Пусть Y и Z - точки пересечения прямой BC с прямыми IbX и IcX соответственно. Докажите, что окружности (ABC) и (XYZ) касаются

Кстати, картинка белая

Задача 75: [ЮМТ2025]

X и Y - точки касания касательных из центра масс треугольника ABC к его вписанной окружности. Докажите, что X и Y изотомически сопряжены в ABC

Ура, еще одна задачка от меня и Дани Игнатьева на ЮМТ

Немного о том, как была придумана эта задача:

Сидел я и придумывал тестовые задачи для отбора в т-геометрию и задался вопросом:

Задача 75 и 3/4: Сколько в треугольнике существует пар изогонально сопряженных точек, обе из которых лежат на вписанной окружности? Тот же вопрос для описанного четырехугольника? (укажите все возможные варианты)

В итоге 2ой вопрос попал в вариант отбора. Но отсюда сразу следует такой естественный вопрос: А сколько таких пар точек для изотомического сопряжения? А для произвольного проективного сопряжения? (изогональное и изотомическое сопряжения это I-сопряжение и M-сопряжение, т.е. частные случаи проективных сопряжений)

Отличие от случая инцентра в том, что инцентр всегда лежит внутри вписанной окружности, а вот точка P при P-сопряжении может быть как внутри, так и вне (да, да, на окружности тоже может быть). Если она внутри, то таких пар точек 3: пересечения прямых, образованных точками пересечения прямых B1C1 с AP, A1B1 с CP, A1C1 с BP, с вписанной окружностью. Если же P снаружи, то добавляется пара точек, являющихся пересечениями поляры P с вписанной окружностью, и сопряженных пар в итоге 4. Отсюда и получилась задача, которая была на финале ЮМТ.

А конструкция с картинки является леммой для доказательства утверждений про колличество пар P-сопряженных точек: зеленые прямые P-сопряжены для верхнего угла <=> пунктирные прямые проходят через синие точки, где синие прямые - это AP и дополняющая AB, AC, AP до гармонической четверки

Задача 76:

Пусть I - инцентр ABC, D - точка касания вписанной с BC, P - проекция I на сер пер к AD. Докажите, что углы BPI и CPI равны

Задача 77:

Дан треугольник ABC с прямым углом A и точка D на его катете AC. Пусть E - отражение A относительно BD. Точка F на CE такова, что DF перпендикулярно BC. Докажите, что прямые AF, DE и BC пересекаются в одной точке.

Задача 78:

Дан гармонический четырехугольник ABCD. Точка K на прямой AB такова, что угол BCK прямой. Прямая KD пересекает AC и (ABC) в точках N и E. H - основание высоты из A на BC, M - середина отрезка AC, F - середина дуги BAC. Оказалось, что четырехугольник BHMF - вписанный. Докажите, что BE = AN

Задача 79:

Парабола с фокусом F касается сторон АВ и АС треугольника АВС, она пересекает сторону ВС в точках M и N, а прямая АF пересекает ВС в точке W.доказать что окружности (МWF) и (NWF) касаются окружности (АВС)