суммы косинусов и кубические уравнения
сегодня кода не будет, а будет математический комментарий к предыдущему посту (и не совсем популярный, сорри)
1.
напомню для начала квадратичный случай
пусть P простое число… и пускай вида 4k+1
квадратичная сумма Гаусса — это способ выразить √P через корни степени P из единицы с разными знаками (если показатель степени — квадратичный вычет mod P, то берем знак +1, для невычета — -1)
можно записать его в виде ∑cos(n² 2π/P)=√P
(например, для p=5: cos(2π/5)=(√5-1)/4, а вся сумма состоит из 4 равных косинусов и единицы)
2.
пускай теперь P=3k+1, а нас интересует тригонометрическая сумма G=∑cos(n³ 2π/P)
Галуа говорит нам, что G — корень кубического уравнения с рациональными коэффициентами, но какого конкретно?
полезно начать не с суммы G, а с кубической суммы Гаусса g
определяется она аналогично квадратичному случаю, но знак +1 теперь получают степени, являющиеся кубическими вычетами, еще два класса — знаки ω и ω² (ω — комплексный кубический корень из единицы)
(другими словами, g — линейная комбинация трех корней искомого уравнения, на которой группа Галуа действует просто умножением на ω)
снова |g|=√P, но теперь что-то хорошее получается при возведении не в квадрат, а в куб: g³=PП, где ПП' — разложение p на простые в Z[ω], а штрих обозначает комплексное сопряжение
3.
вернемся к тригонометрической сумме
G=g+g', поэтому (пользуясь описанными выше свойствами g)
G³=g³+g'³+3gg'(g+g')=P(П+П')+3PG,
т.е. G корень кубического уравнения x³-3Px-AP, где A=2ReП
чтобы получить уравнение буквально на суммы, которые рассматривались в предыдущем посте, нужно еще сделать замену x=-3t+1
4.
если хочется вычислить A без использования арифметики в Z[ω], то можно воспользоваться тем, что если P=ПП' в Z[ω], A=2ReП, то
4P=A²+27B²
такое представление единственно… с точностью до знаков; “наше” A — это то, которое дает остаткок 1 mod 3 (это вопрос про знак гауссовой суммы, который выше был заметен под ковер… там пусть и остается)
можно описать A и по-другому: количество решений по модулю P уравнения X³+Y³=1 равно P-2+A
5.
дискриминант уравнения x³-3Px-AP=0 как раз равен (27PB)²
вообще через корни из единицы (или, если угодно, через триг. функции рац. аргумента) можно выразить решения тех и только тех неприводимых кубических уравнений с рациональными коэффициентами, у которых дискриминант является полным квадратом (аналог для произвольной степени: группа Галуа должна быть абелевой)
уравнение x³=P, например, не подходит, а вот наше — вполне себе
надеюсь, что в написанном выше можно уже увидеть контуры рецепта для решения «в косинусах» произвольного кубического уравнения с квадратным дискриминантом
6.
если P=9m²-3m+1, то 4P=(3m-2)²+27m². В этом случае свободный член уравнения на триг. суммы является полным кубом (числа m, собственно) и формула Рамануджана для суммы кубических корней из корней уравнения дает особенно простой ответ:
2S³ = 3³√(mP)-6m+1
например, для P=73 имеем m=3 и ответ ³√((3³√219-17)/2); для P=31 имеем m=-2 и опечатку в заметке в Мат. просвещении
сегодня кода не будет, а будет математический комментарий к предыдущему посту (и не совсем популярный, сорри)
1.
напомню для начала квадратичный случай
пусть P простое число… и пускай вида 4k+1
квадратичная сумма Гаусса — это способ выразить √P через корни степени P из единицы с разными знаками (если показатель степени — квадратичный вычет mod P, то берем знак +1, для невычета — -1)
можно записать его в виде ∑cos(n² 2π/P)=√P
(например, для p=5: cos(2π/5)=(√5-1)/4, а вся сумма состоит из 4 равных косинусов и единицы)
2.
пускай теперь P=3k+1, а нас интересует тригонометрическая сумма G=∑cos(n³ 2π/P)
Галуа говорит нам, что G — корень кубического уравнения с рациональными коэффициентами, но какого конкретно?
полезно начать не с суммы G, а с кубической суммы Гаусса g
определяется она аналогично квадратичному случаю, но знак +1 теперь получают степени, являющиеся кубическими вычетами, еще два класса — знаки ω и ω² (ω — комплексный кубический корень из единицы)
(другими словами, g — линейная комбинация трех корней искомого уравнения, на которой группа Галуа действует просто умножением на ω)
снова |g|=√P, но теперь что-то хорошее получается при возведении не в квадрат, а в куб: g³=PП, где ПП' — разложение p на простые в Z[ω], а штрих обозначает комплексное сопряжение
3.
вернемся к тригонометрической сумме
G=g+g', поэтому (пользуясь описанными выше свойствами g)
G³=g³+g'³+3gg'(g+g')=P(П+П')+3PG,
т.е. G корень кубического уравнения x³-3Px-AP, где A=2ReП
чтобы получить уравнение буквально на суммы, которые рассматривались в предыдущем посте, нужно еще сделать замену x=-3t+1
4.
если хочется вычислить A без использования арифметики в Z[ω], то можно воспользоваться тем, что если P=ПП' в Z[ω], A=2ReП, то
4P=A²+27B²
такое представление единственно… с точностью до знаков; “наше” A — это то, которое дает остаткок 1 mod 3 (это вопрос про знак гауссовой суммы, который выше был заметен под ковер… там пусть и остается)
можно описать A и по-другому: количество решений по модулю P уравнения X³+Y³=1 равно P-2+A
5.
дискриминант уравнения x³-3Px-AP=0 как раз равен (27PB)²
вообще через корни из единицы (или, если угодно, через триг. функции рац. аргумента) можно выразить решения тех и только тех неприводимых кубических уравнений с рациональными коэффициентами, у которых дискриминант является полным квадратом (аналог для произвольной степени: группа Галуа должна быть абелевой)
уравнение x³=P, например, не подходит, а вот наше — вполне себе
надеюсь, что в написанном выше можно уже увидеть контуры рецепта для решения «в косинусах» произвольного кубического уравнения с квадратным дискриминантом
6.
если P=9m²-3m+1, то 4P=(3m-2)²+27m². В этом случае свободный член уравнения на триг. суммы является полным кубом (числа m, собственно) и формула Рамануджана для суммы кубических корней из корней уравнения дает особенно простой ответ:
2S³ = 3³√(mP)-6m+1
например, для P=73 имеем m=3 и ответ ³√((3³√219-17)/2); для P=31 имеем m=-2 и опечатку в заметке в Мат. просвещении
Telegram
Компьютерная математика Weekly
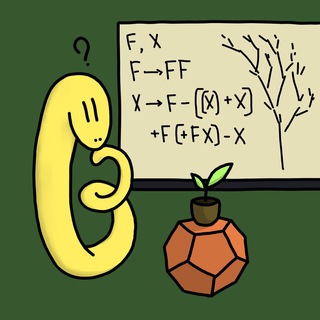
на картинке сверху — тождества¹ из заметки С.Маркелова в Мат. просвещении, и там предлагается придумать обобщения
¹ там только есть опечатка… найдите
программа в комментариях — говорит, суммы каких косинусов надо взять для произвольного p вида 3k+1, а также…
¹ там только есть опечатка… найдите
программа в комментариях — говорит, суммы каких косинусов надо взять для произвольного p вида 3k+1, а также…
👍11❤1
L-системы, или Как нарисовать снежинку и дерево
1.
начнем со слова A и дальше будем итерировать такие замены: A→AB, B→A (на каждой итерации одновременно заменяются все буквы по указанным правилам)
будут получаться всё большие отрезки интересного слова Фибоначчи — про него можно прочитать в статье Вити Клепцына в «Квантике» (№№5-6 за 2020 год)
такого рода правила (“L-системы”) легко реализовать — например, так:
2.
такого рода правила порождают слова с фрактальной структурой… так что можно попробовать превратить их во фрактальные картинки
можно начать, например, со снежинки Коха: мы стартуем с правильного треугольника, а дальше на каждой итерации заменяем каждый отрезок на зубец («_ → _/\_»)
это можно закодировать так:
где “F” означает «идем вперед и рисуем отрезок», а “+” и “-” — изменения направления
(про такое, кстати, тоже писали в «Квантике»: Валя Кириченко и Владлен Тиморин объясняли, как это связано со словом Туэ-Морса и проч.)
осталось это реально нарисовать — например, при помощи matplotlib:
для 4 итераций получается буквально картинка сверху
можно в таком духе генерировать и, скажем, несамопересекающиеся кривые, приближающиеся к заполнению квадрата — например, вот так:
(продолжение следует)
1.
начнем со слова A и дальше будем итерировать такие замены: A→AB, B→A (на каждой итерации одновременно заменяются все буквы по указанным правилам)
будут получаться всё большие отрезки интересного слова Фибоначчи — про него можно прочитать в статье Вити Клепцына в «Квантике» (№№5-6 за 2020 год)
такого рода правила (“L-системы”) легко реализовать — например, так:
def lsystem(seed,rules,iterations):
for _ in range(iterations):
seed = "".join(
rules[letter] if letter in rules else letter
for letter in seed)
return seed
print(lsystem("A",{"A":"AB","B":"A"},5))
2.
такого рода правила порождают слова с фрактальной структурой… так что можно попробовать превратить их во фрактальные картинки
можно начать, например, со снежинки Коха: мы стартуем с правильного треугольника, а дальше на каждой итерации заменяем каждый отрезок на зубец («_ → _/\_»)
это можно закодировать так:
snowflake = lsystem("F++F++F",{"F":"F-F++F-F"},4)где “F” означает «идем вперед и рисуем отрезок», а “+” и “-” — изменения направления
(про такое, кстати, тоже писали в «Квантике»: Валя Кириченко и Владлен Тиморин объясняли, как это связано со словом Туэ-Морса и проч.)
осталось это реально нарисовать — например, при помощи matplotlib:
import math
import matplotlib.pyplot as plt
def turtleprint(string,alpha0=0,alpha=90,step=1):
fig = plt.figure()
fig.set_size_inches(6,6)
ax = fig.gca()
ax.set_aspect('equal')
x,y = 0,0
heading = alpha0
for command in string:
if command == "F":
x0,y0 = x,y
x = x0 + step*math.cos(math.radians(heading))
y = y0 + step*math.sin(math.radians(heading))
plt.plot([x0,x],[y0,y],color='k')
if command == "+":
heading += alpha
if command == "-":
heading -= alpha
plt.axis('off')
plt.show()
для 4 итераций получается буквально картинка сверху
можно в таком духе генерировать и, скажем, несамопересекающиеся кривые, приближающиеся к заполнению квадрата — например, вот так:
turtleprint(lsystem("-L",{"L":"LF+RFR+FL-F-LFLFL-FRFR+","R":"-LFLF+RFRFR+F+RF-LFL-FR"},4))
(продолжение следует)
🔥12👍6
L-системы, или Как нарисовать снежинку и дерево
(продолжение, начало выше)
биолог Аристид Линденмайер в конце 1960-х придумал L-системы именно как модель для роста растений — и невозможно не написать про это два слова
сразу скажу, что есть отличная книжка Prusinkiewicz, Lindenmayer. The Algorithmic Beauty of Plants, http://algorithmicbotany.org/papers/#abop (спасибо Никите С. и Роме Г., советовавшим эту книжку) — и там все подробно step by step объясняется, лучшее мб вместо поста ее и читать )
===
3.
в предыдущем посте мы генерировали строки и смотрели на них как на описания путей (символ F означает «двигаться вперед», повороты кодируются символами + и -)
если хочется рисовать деревья, то полезно добавить какую-то возможность ветвления
для этого добавим такое правило для обработки символов [ и ]: после рисования фрагмента в квадратных скобках «черепашка» возвращается туда, где была в его начале
технически для этого в функцию turtleprint добавим
тогда дерево можно нарисовать в духе
(стартуем с отрезка, на каждом шаге заменяем отрезок на цепочку из двух с растущими из середины в обе стороны ветками; на рисунке показано всего 2 шага)
получается, правда, такое совсем уж математическое дерево… чтобы сделать его более растительным, можно сделать два вида “клеток” — "F" пусть будет просто расти, а из "X" пусть происходит еще ветвление в разные стороны
уже не так плохо, но слишком симметрично… перекосить можно так, скажем:
(код целиком положу в комментарии)
***
(не слишком сложными) L-системами можно пользоваться и прямо в техе (в tikz есть для этого бибиотека):
но в питоне, конечно, легче менять любые правила игры по своему желанию
===
вижу иногда, как люди постят generative art, где код умещается примерно в один твит, а на картинках облака летят, деревья растут, вселенные встают и рушатся, и всё такое
здесь вещи довольно примитивные, но всё-таки от того, что вот такая одна строчка фактически рисует узнаваемое дерево (ну хорошо, куст), и вообще от темы в целом — такого же рода вайбы
(продолжение, начало выше)
биолог Аристид Линденмайер в конце 1960-х придумал L-системы именно как модель для роста растений — и невозможно не написать про это два слова
сразу скажу, что есть отличная книжка Prusinkiewicz, Lindenmayer. The Algorithmic Beauty of Plants, http://algorithmicbotany.org/papers/#abop (спасибо Никите С. и Роме Г., советовавшим эту книжку) — и там все подробно step by step объясняется, лучшее мб вместо поста ее и читать )
===
3.
в предыдущем посте мы генерировали строки и смотрели на них как на описания путей (символ F означает «двигаться вперед», повороты кодируются символами + и -)
если хочется рисовать деревья, то полезно добавить какую-то возможность ветвления
для этого добавим такое правило для обработки символов [ и ]: после рисования фрагмента в квадратных скобках «черепашка» возвращается туда, где была в его начале
технически для этого в функцию turtleprint добавим
stack = []
…
if command == "[":
stack.append((x,y,heading))
if command == "]":
x,y,heading = stack.pop()
тогда дерево можно нарисовать в духе
seed="F"
rules={"F": "F[+F][-F]F"}
(стартуем с отрезка, на каждом шаге заменяем отрезок на цепочку из двух с растущими из середины в обе стороны ветками; на рисунке показано всего 2 шага)
получается, правда, такое совсем уж математическое дерево… чтобы сделать его более растительным, можно сделать два вида “клеток” — "F" пусть будет просто расти, а из "X" пусть происходит еще ветвление в разные стороны
seed="X"
rules={"F": "FF", "X": "F[+X][-X]FX"}
уже не так плохо, но слишком симметрично… перекосить можно так, скажем:
seed="X"
rules={"F": "FF", "X": "F-[[X]+X]+F[+FX]-X"}
(код целиком положу в комментарии)
***
(не слишком сложными) L-системами можно пользоваться и прямо в техе (в tikz есть для этого бибиотека):
\usetikzlibrary{lindenmayersystems}
\begin{tikzpicture}[rotate=65]
\draw[green!60!black] l-system[l-system={axiom=F,rule set={F -> F[+F]F[-F]}, order=4, angle=25,step=3pt}];
\end{tikzpicture}
но в питоне, конечно, легче менять любые правила игры по своему желанию
===
вижу иногда, как люди постят generative art, где код умещается примерно в один твит, а на картинках облака летят, деревья растут, вселенные встают и рушатся, и всё такое
здесь вещи довольно примитивные, но всё-таки от того, что вот такая одна строчка фактически рисует узнаваемое дерево (ну хорошо, куст), и вообще от темы в целом — такого же рода вайбы
Посмотрим на то, для каких простых P уравнение X²=D разрешимо в остатках по модулю P.
На компьютерных экспериментах хорошо видно, что возникает удивительная периодичность — вот, например, для D=7 (для непростых модулей вместо ответа печатается точка):
Ответ всегда зависит только от остатка P mod 4D — это квадратичный закон взаимности (в форме, открытой Эйлером).
Можно было бы надеяться, что похожая история будет и в кубическом случае… но нет, ничего похожего. Простые P, для которых уравнение X³=2 (например) разрешимо mod P, выглядят хаотично, никакого периода нет. Единственная относительно видная закономерность — что доля простых, для которых X²=D разрешимо, всегда (ну если D не куб ) примерно 2/3.
Но можно посмотреть и на другие кубические многочлены — и иногда ответ снова определяется остатком P по какому-то модулю. Например:
Можно подумать, чем одни кубические многочлены отличаются от других (если гадать станет невыносимо, топосчитайте дискриминанты ).
===
Это всё можно и в экселе делать — но в комментарии положу небольшую программу на питоне.
А для математического контекста — пусть здесь будет популярная лекция Фрэнка Калегари на ICM-2022: https://youtu.be/EDsK-8SBx-g (там как раз с таких вопросов все и начинается)
На компьютерных экспериментах хорошо видно, что возникает удивительная периодичность — вот, например, для D=7 (для непростых модулей вместо ответа печатается точка):
x²=7 mod p
apparent (weak) period is 28
..++.-.+...-.-...-.+...-....
.+.+.....+...-.-...+.....+..
...+.-.....-...-.-.....-...+
.....-.......-...-.+...-.+..
.+.............-...+.....+.+
.........+.-.....-.....-...+
.....-.....-.-.........-.+..
.+.+...........-...........+
...+.-...+.....-.-.........+
.....-.....-.....-.+.....+..
Ответ всегда зависит только от остатка P mod 4D — это квадратичный закон взаимности (в форме, открытой Эйлером).
Можно было бы надеяться, что похожая история будет и в кубическом случае… но нет, ничего похожего. Простые P, для которых уравнение X³=2 (например) разрешимо mod P, выглядят хаотично, никакого периода нет. Единственная относительно видная закономерность — что доля простых, для которых X²=D разрешимо, всегда (ну если D не куб ) примерно 2/3.
x³=2 mod p
no apparent period
..++.+.-...+.-...+.-...+.....+.+.....-...+.+...+.....+.....+.-.....-...+.-.....-...+.....+.......-...+.-...+.+...+.............+...+.....+.-.........+.-.....+.....-...+.....+.....+.-.........+.-...+.-...........-...........+...+.+...+.....+.-.........+.....+.....+.....+.-.....+...+.+.........+.............(…)
+: 112 -: 56 rat: 0.67
Но можно посмотреть и на другие кубические многочлены — и иногда ответ снова определяется остатком P по какому-то модулю. Например:
x³-9x-9=0 mod p
apparent (weak) period is 9
..-+.-.-.
..-.-...+
.+...-...
..-.-....
.+...-.-.
..-.....+
.....-.-.
....-...+
.+.....-.
..-.....+
.......-.
.
+: 8 -: 17 rat: 0.32
x³-x²-4x-1=0 mod p
apparent (weak) period is 13
..--.+.-...-.
+...-.-...-..
...-.+.....-.
..-.-...+....
.+.....-.-...
..-...-.+....
.+...+.....-.
......-...-.+
...-.+...-...
..........-..
.+.....-.-...
......-.+....
.+.....-...-.
....-.....-.+
.........-.-.
..-.-
+: 14 -: 32 rat: 0.3
Можно подумать, чем одни кубические многочлены отличаются от других (если гадать станет невыносимо, то
===
Это всё можно и в экселе делать — но в комментарии положу небольшую программу на питоне.
А для математического контекста — пусть здесь будет популярная лекция Фрэнка Калегари на ICM-2022: https://youtu.be/EDsK-8SBx-g (там как раз с таких вопросов все и начинается)
YouTube
Frank Calegari: 30 years of modularity: number theory since the proof of Fermat's Last Theorem
Enjoy the videos and music you love, upload original content, and share it all with friends, family, and the world on YouTube.
👍7
0.
здесь уже обсуждалось, что если функция достаточно хорошая, то уравнение f(x)=0 можно быстро приближенно решать при помощи метода Ньютона
но если посмотреть на это не локально рядом с нулем, а глобально, то картинка становится более сложной
на картинках выше показано, как работает метод Ньютона для нахождения корня уравнения z⁴-1=0 [на комплексной плоскости]
(какой-нибудь код будет в комментариях)
1.
на левой картинке — сколько итераций надо сделать, чтобы подойти к корню ближе чем на 10^{-6}; видно, что обычно действительно достаточно пары итераций — но иногда даже для вроде бы небольших чисел требуются многие десятки итераций
возникает вопрос, так ли хорош метод Ньютона
цитата — из статьи А.Гасникова https://zanauku.mipt.ru/2023/01/19/ot-nyutona-do-kovaleva/ (статья популярная, но там есть ссылки и на статьи с подробностями)
2.
на правой картинке — показано, к какому из комплексных корней сходится метод Ньютона, стартующий в данной точке
получается пример невозможной, казалось бы, ситуации: такие 4 области плоскости, что любая точка границы одной из них лежит на границе всех 4 («в любой точке границы граничат сразу 4 страны»)
видно, что бывает затруднительно предсказать, к какому из корней сойдется метод Ньютона (рядом с общей границей множеств возникает фрактальная структура из анклавов-внутри анклавов-внутри анклавов…)
мне кажется, впервые узнал про такое (как и про многое другое в математике) из рассказов Вити Клепцына — спасибо ему
***
ну или можно никаких объяснений не читать, просто посмотреть на красивые картинки… еще больше картинок у 3Blue1Brown: https://youtu.be/-RdOwhmqP5s
здесь уже обсуждалось, что если функция достаточно хорошая, то уравнение f(x)=0 можно быстро приближенно решать при помощи метода Ньютона
если x — приближенное значение корня, то рядом ним график функции недалеко ушел от касательной, поэтому в качестве следующего приближения можно взять пересечения касательной с нулем, т.е. x→x-f(x)/f'(x)
и в некоторой окрестности корня метод Ньютона, если производная в этом корне не равна 0, сходится очень быстро: за итерацию погрешность ~возводится в квадрат
но если посмотреть на это не локально рядом с нулем, а глобально, то картинка становится более сложной
на картинках выше показано, как работает метод Ньютона для нахождения корня уравнения z⁴-1=0 [на комплексной плоскости]
(какой-нибудь код будет в комментариях)
1.
на левой картинке — сколько итераций надо сделать, чтобы подойти к корню ближе чем на 10^{-6}; видно, что обычно действительно достаточно пары итераций — но иногда даже для вроде бы небольших чисел требуются многие десятки итераций
возникает вопрос, так ли хорош метод Ньютона
Грубо говоря, Немировским было показано, что метод Ньютона локально является оптимальным. Под «локально» имеется в виду, что точку старта метода нужно брать достаточно близко к решению. А что будет, если точку старта (начальное приближение) не удастся подобрать достаточно близко к решению? Ведь мы не знаем, где решение. Собственно, в этом же и задача — найти решение! Какой метод будет оптимальным без таких оговорок?
цитата — из статьи А.Гасникова https://zanauku.mipt.ru/2023/01/19/ot-nyutona-do-kovaleva/ (статья популярная, но там есть ссылки и на статьи с подробностями)
2.
на правой картинке — показано, к какому из комплексных корней сходится метод Ньютона, стартующий в данной точке
получается пример невозможной, казалось бы, ситуации: такие 4 области плоскости, что любая точка границы одной из них лежит на границе всех 4 («в любой точке границы граничат сразу 4 страны»)
видно, что бывает затруднительно предсказать, к какому из корней сойдется метод Ньютона (рядом с общей границей множеств возникает фрактальная структура из анклавов-внутри анклавов-внутри анклавов…)
мне кажется, впервые узнал про такое (как и про многое другое в математике) из рассказов Вити Клепцына — спасибо ему
***
ну или можно никаких объяснений не читать, просто посмотреть на красивые картинки… еще больше картинок у 3Blue1Brown: https://youtu.be/-RdOwhmqP5s
🔥9❤1
дайджест комментариев и прочего
перебирал еще на компутере кое-что из задач, рассматривавшихся для Матпраздника, но подобностей, естественно, не будет — вместо этого будет подборка разного
1.
в обсуждении представимости чисел в виде суммы двух квадратов Ф.Бахарев поднял тему эффективного нахождения таких представлений — а оказывается, про это была статья в Мат. Просвещении: https://www.mathedu.ru/text/mp_2006_v10/p190/
для алгоритма из статьи нужно, правда, сначала найти корень из -1 mod p — это Федя так учит делать:
а Р.Гусарев поделился статьей про быстрое нахождения представления любого числа в виде суммы 4 квадратов: https://campus.lakeforest.edu/trevino/finding4squares.pdf (и там не обходится, естественно, без кватернионов)
2.
в обсуждении суммы обратных простых М.Трошкин рассказал, что если складывать обратные только к простым числам-близнецам, то сумма сходится (хотя и очень медленно)
и знаменитый баг в процессорах Пентиум, который стоил Интелу полмиллиарда долларов в 1994 году, нашли, оказывается, ровно при попытке поточнее вычислить сумму этого ряда
баг, кстати, связан с (неправильным) ускорением деления — так что эта история в каком-то смысле примыкает и к посту про быстрое деление (хотя алгоритм там другой)
3.
Л.Петров у себя в канале делится демонстрацией того, как себя ведут собственные значения случайных матриц: https://lpetrov.cc/simulations/2025-01-28-goe/
(и повод для комп. экспериментов хороший, и хотелось бы, конечно, оформлять все столь же удобно и красиво)
наконец, у канала (и прикрепленного к нему чата) появился юзерпик — спасибо Тане Кор. за картинки
перебирал еще на компутере кое-что из задач, рассматривавшихся для Матпраздника, но подобностей, естественно, не будет — вместо этого будет подборка разного
1.
в обсуждении представимости чисел в виде суммы двух квадратов Ф.Бахарев поднял тему эффективного нахождения таких представлений — а оказывается, про это была статья в Мат. Просвещении: https://www.mathedu.ru/text/mp_2006_v10/p190/
для алгоритма из статьи нужно, правда, сначала найти корень из -1 mod p — это Федя так учит делать:
проще всего найти квадратичный невычет и возвести его быстрым возведением в степень (p-1)/2. невычет можно либо случайно искать (вероятность 1/2), либо просто перебирать первые простые и считать символ Лежандра. если гипотеза Римана верна, то найдется очень быстро. но на практике вообще среди первых нескольких простых обычно есть
а Р.Гусарев поделился статьей про быстрое нахождения представления любого числа в виде суммы 4 квадратов: https://campus.lakeforest.edu/trevino/finding4squares.pdf (и там не обходится, естественно, без кватернионов)
2.
в обсуждении суммы обратных простых М.Трошкин рассказал, что если складывать обратные только к простым числам-близнецам, то сумма сходится (хотя и очень медленно)
и знаменитый баг в процессорах Пентиум, который стоил Интелу полмиллиарда долларов в 1994 году, нашли, оказывается, ровно при попытке поточнее вычислить сумму этого ряда
баг, кстати, связан с (неправильным) ускорением деления — так что эта история в каком-то смысле примыкает и к посту про быстрое деление (хотя алгоритм там другой)
3.
Л.Петров у себя в канале делится демонстрацией того, как себя ведут собственные значения случайных матриц: https://lpetrov.cc/simulations/2025-01-28-goe/
(и повод для комп. экспериментов хороший, и хотелось бы, конечно, оформлять все столь же удобно и красиво)
наконец, у канала (и прикрепленного к нему чата) появился юзерпик — спасибо Тане Кор. за картинки
👍7🔥7❤2💯1
в промежутке между разным — нарисовал картинку с простыми числами в Z[i]
напомню, что p=4k+3 остаются простыми в Z[i], а p=4k+1 (и p=2) разлагаются в произведение двух множителей нормы p
(это и использует программа в комментариях)
при первом взгляде на картинку показалось, что что-то их очень много… прикинем: в круге радиуса R можно ожидать ~R/log(R) простых «первого вида» и ~R²/log(R) простых «второго вида»¹
и они на удалении от начала координат достаточно равномерно распределены², в частности, в области размера больше ~log(R) обычно видны отмеченные точки (а если мы смотрим на картинке одного физического размера на всё большую часть плоскости, то эти области становятся очень маленькими, визуально точки «есть везде», хоть и с не очень большой плотностью)
¹ забавно, что простых вида 4k+1 и 4k+3 в целых числах примерно поровну, но когда в Z[i] мы фиксируем ограничение на норму, то простых, происходящих из 4k+1, видно радикально больше
² равномерность распределения аргументов доказал, говорят, Гекке в 1919 году — вот современное обсуждение: https://arxiv.org/abs/1705.07498
напомню, что p=4k+3 остаются простыми в Z[i], а p=4k+1 (и p=2) разлагаются в произведение двух множителей нормы p
(это и использует программа в комментариях)
при первом взгляде на картинку показалось, что что-то их очень много… прикинем: в круге радиуса R можно ожидать ~R/log(R) простых «первого вида» и ~R²/log(R) простых «второго вида»¹
и они на удалении от начала координат достаточно равномерно распределены², в частности, в области размера больше ~log(R) обычно видны отмеченные точки (а если мы смотрим на картинке одного физического размера на всё большую часть плоскости, то эти области становятся очень маленькими, визуально точки «есть везде», хоть и с не очень большой плотностью)
¹ забавно, что простых вида 4k+1 и 4k+3 в целых числах примерно поровну, но когда в Z[i] мы фиксируем ограничение на норму, то простых, происходящих из 4k+1, видно радикально больше
² равномерность распределения аргументов доказал, говорят, Гекке в 1919 году — вот современное обсуждение: https://arxiv.org/abs/1705.07498
👍5🔥3
справа можно видеть фрагмент квазипериодического замощения плоскости
в нем участвуют равнобедренные треугольники с углами при вершине π/5 (красные, «A») и 3π/5 (синие, «B»)
они замечательны тем, что A можно разбить на уменьшенные копии A,B,A, ну а B можно разбить на уменьшенные копии A,B — и если начать с А и итерировать такие замены, то можно думать, что мы собираем из треугольников A и B всё большую копию треугольника¹ A (в левой половинке картинки — первая пара итераций)
такая мозаика — одна из вещей, про которые при создании канала думал, что хорошо бы ее нарисовать, но не очень понятно как
а вечером подумал, что это просто L-система — только параметрическая: кроме буквы A/B нужно помнить, как именно треугольник расположен на плоскости (и правила замены эти параметры должны правильно менять) — так что можно быстренько реализовать
¹ а чтобы получить замощение плоскости, можно, скажем, стартовать с 10 треугольников A с общей вершиной
положение треугольника решил хранить в виде пары комплексных чисел² (преобразования z→az+b, переводящего эталонный треугольник в наш) и написал такой шаг для получающейся параметрической l-системы:
по сути на этом все! — остается только дописать код для рисования треугольничков… ну программа целиком будет в комментариях
² уже засомневался, так ли это удачно — потому что для настоящей мозаики Пенроуза треугольники полезно и переворачивать
в нем участвуют равнобедренные треугольники с углами при вершине π/5 (красные, «A») и 3π/5 (синие, «B»)
они замечательны тем, что A можно разбить на уменьшенные копии A,B,A, ну а B можно разбить на уменьшенные копии A,B — и если начать с А и итерировать такие замены, то можно думать, что мы собираем из треугольников A и B всё большую копию треугольника¹ A (в левой половинке картинки — первая пара итераций)
такая мозаика — одна из вещей, про которые при создании канала думал, что хорошо бы ее нарисовать, но не очень понятно как
а вечером подумал, что это просто L-система — только параметрическая: кроме буквы A/B нужно помнить, как именно треугольник расположен на плоскости (и правила замены эти параметры должны правильно менять) — так что можно быстренько реализовать
¹ а чтобы получить замощение плоскости, можно, скажем, стартовать с 10 треугольников A с общей вершиной
положение треугольника решил хранить в виде пары комплексных чисел² (преобразования z→az+b, переводящего эталонный треугольник в наш) и написал такой шаг для получающейся параметрической l-системы:
phi = (math.sqrt(5)+1)/2
rot = math.cos(math.pi/5)+math.sin(math.pi/5)*1j
def step(state):
for atom in state:
c, a, b = atom
if c=='A':
yield ('A',a,b*phi)
yield ('B',a*(rot**4),(a+b)*phi)
yield ('A',a*(rot**3),(a+b)*phi)
if c=='B':
yield ('A',a,b*phi)
yield ('B',a*(rot**4),(a+b)*phi)
state = [('A',rot**i,0+0j) for i in range(10)]
for _ in range(6):
state = step(state)
по сути на этом все! — остается только дописать код для рисования треугольничков… ну программа целиком будет в комментариях
² уже засомневался, так ли это удачно — потому что для настоящей мозаики Пенроуза треугольники полезно и переворачивать
👍6❤3🔥2
This may depend on your specific area, but in bijective combinatorics you have to believe in miracles! Otherwise you can never fully appreciate prior work, and can never let yourself loose enough to discover new miracles. To give just one example, the RSK correspondence is definitely on everyone’s the top ten list of miracles in the area. By now there are at least half a dozen ways to understand and explain it, but I still consider RSK to be a miracle.
(из недавнего поста Игоря Пака)
про RSK — невозможно, кажется, поспорить
в порядке мелких развлечений на глубоких местах — написал пока самую примитивную реализацию RSK (в комментариях)
она берет последовательность целых чисел и расставляет правильным образом по клеткам таблицы P
в т.ч. длина первой строки P — как у самой длинной (нестрого) возрастающей подпоследовательности, а длина первого столбца — как у самой длинной (строго) убывающая подпоследовательности (бесплатное следствие — теорема Эрдеша-Секереша: в последовательности длины nm+1 либо первая длиннее n, либо последняя длиннее m)
заодно можно компьютерно убедиться в том, что для случайной перестановки N элементов самая длинная возрастающая подпоследовательность имеет длину ~2√N (как доказали Вершик-Керов, Логан-Шепп)
соответствие RSK связано не только с монотонными подпоследовательностями, но и с подсчетом плоских разбиений, и с теорией представлений, и с симметрическими функциями, со всем на свете… надеюсь, будут про это продолжения
👍9
этот канал существует чуть больше месяца, уже до какой-то степени стал виден стиль и круг тем — а с другой стороны, всё это еще не застыло
в комментариях к этому посту предлагаю обмениваться идеями сюжетов и форм, тематическими ссылками и проч.
в комментариях к этому посту предлагаю обмениваться идеями сюжетов и форм, тематическими ссылками и проч.
кажется, что веб-страница доступна гораздо большему числу людей, чем программа на питоне
попросил chatgpt сконвертировать реализацию RSK из прошлого поста в javanoscript, поправил минимально оформление — и пожалуйста, вот веб-версия:
https://dev.mccme.ru/~merzon/compmath/RSK.html
если для экспериментов нужен повод — поучительно посмотреть, скажем, что происходит при этом соответствии с инволюциями
попросил chatgpt сконвертировать реализацию RSK из прошлого поста в javanoscript, поправил минимально оформление — и пожалуйста, вот веб-версия:
https://dev.mccme.ru/~merzon/compmath/RSK.html
если для экспериментов нужен повод — поучительно посмотреть, скажем, что происходит при этом соответствии с инволюциями
🔥12👍4👏1
Компьютерная математика Weekly pinned «этот канал существует чуть больше месяца, уже до какой-то степени стал виден стиль и круг тем — а с другой стороны, всё это еще не застыло в комментариях к этому посту предлагаю обмениваться идеями сюжетов и форм, тематическими ссылками и проч.»
Ваня Яковлев напомнил задачу о разборчивой невесте — вот формулировка из брошюры С.М.Гусейна-Заде:
естественная стратегия для принцессы состоит из двух стадий:
1) на первых скольких-то претендентов только смотреть (сразу отказывать им, но запоминать, насколько они были хороши)
2) из оставшихся претендентов — выходить замуж за первого же, кто будет лучше всех ранее виденных
но остается вопрос, как выбрать момент s (долю от 0 до 1) перехода от первой стадии ко второй — и здесь вполне можно поставить компьютерный эксперимент:
попросил и из этого chatgpt сделать html-версию и мгновенно… получил программу с неправильной генерацией случайной перестановки
но вроде всё удалось исправить — и по ссылке https://dev.mccme.ru/~merzon/compmath/bride.html можно выбрать момент s и посмотреть, насколько успешна ваша стратегия
для меня сюрпризом стало, что в реальности разница между теоретически лучшим вариантом (ну почитайте Гусейна-Заде! ) и наивным s=50% (или, скажем, s=25%) ничтожна
(тут, кстати, легко грубо прикинуть: вероятность того, что лучший кандидат во второй половине, а second best в первой, — уже 1/4, так что s=1/2 приводит к успеху с вероятностью больше 25%)
можно дальше, конечно, экспериментировать с разными обобщениями (принцессу устравает не только лучший, но и второй… принцессу разные результаты устраивают в разной степени… принцессе тяжело долго ждать… и т.д.)
В некотором царстве, в некотором государстве пришло время принцессе выбирать себе жениха. В назначенный день явились 1000 царевичей. Их построили в очередь в случайном порядке и стали по одному приглашать к принцессе. Про любых двух претендентов принцесса, познакомившись с ними, может сказать, какой из них лучше. Познакомившись с претендентом, принцесса может либо принять предложение(и тогда выбор сделан навсегда), либо отвергнуть его (и тогда претендент потерян: царевичи гордые и не возвращаются).Какой стратегии должна придерживаться принцесса, чтобы с наибольшей вероятностью выбрать лучшего?
естественная стратегия для принцессы состоит из двух стадий:
1) на первых скольких-то претендентов только смотреть (сразу отказывать им, но запоминать, насколько они были хороши)
2) из оставшихся претендентов — выходить замуж за первого же, кто будет лучше всех ранее виденных
но остается вопрос, как выбрать момент s (долю от 0 до 1) перехода от первой стадии ко второй — и здесь вполне можно поставить компьютерный эксперимент:
def concrete_test(s,sigma):
N = len(sigma)
n = math.floor(N*s)
m = max(sigma[:n]) if n>0 else -1
# пропустили долю s кандидатов
# и ждем первого, лучше всех предыдущих
while n<N and sigma[n]<=m: n += 1
return n<N and sigma[n]==N-1 # нашли максимум?
def random_tests(s,N,T):
sigma = np.array(range(N))
wins = 0
for _ in range(T):
random.shuffle(sigma)
if concrete_test(s,sigma): wins += 1
return wins/T
попросил и из этого chatgpt сделать html-версию и мгновенно… получил программу с неправильной генерацией случайной перестановки
но вроде всё удалось исправить — и по ссылке https://dev.mccme.ru/~merzon/compmath/bride.html можно выбрать момент s и посмотреть, насколько успешна ваша стратегия
для меня сюрпризом стало, что в реальности разница между теоретически лучшим вариантом (
(тут, кстати, легко грубо прикинуть: вероятность того, что лучший кандидат во второй половине, а second best в первой, — уже 1/4, так что s=1/2 приводит к успеху с вероятностью больше 25%)
можно дальше, конечно, экспериментировать с разными обобщениями (принцессу устравает не только лучший, но и второй… принцессу разные результаты устраивают в разной степени… принцессе тяжело долго ждать… и т.д.)
👍11❤3🔥2
будем считать количество трехмерных диаграмм Юнга («фигур из кубиков в углу комнаты», между кубиком и каждой из трех стенок не должно быть пустот) данного объема
их оказывается столько же, сколько матриц из целых неотрицательных чисел, если число в клетке (i, j) считать с весом i+j-1 (так что, например, производящая функция для всех трехмерных диаграмм равна Π(1-q^i)^{-i})
это может показаться смутно гармоничным (если в плоском разбиении на клетке (i,j) лежит кубик, то и на клетках (i',j) и (i,j') при всех i'<i и j'<j лежат кубики… и всего таких кубиков минимум i+j-1…), но если пытаться придумать конкретную биекцию, возникает ощущение магии
это тоже магия соответствия RSK
выше была версия RSK, переводящая перестановку в пару стандартных таблиц одинаковой формы… здесь используется версия, переводящая произвольную матрицу из целых неотрицательных чисел в пару полустандартных таблиц одинаковой формы — а если рассечь трехмерную диаграмму Юнга по диагонали то как раз получится обычная диаграмма Юнга, в клетки которой можно записать, сколько кубкиков растет в одну сторону, а можно — сколько в другую
реализация — в комментариях
дальше решил попросить chatgpt сделать веб-версию с рисованием кубиков — и это была прямо суперразочаровывающая трата времени (все делает неправильно, не способен реагировать на замечания, да еще при доработке рисования кубиков все время норовит удалить собственно RSK)
плюнул и за 10 минут написал matplotlib-рисование кубиков (результат на картинке)… ну может еще и сделаю веб-версию, не знаю
***
у нас с Мишей Берштейном есть текст в МатПросвещении, где рассказывается в том числе про подсчет трехмерных диаграмм Юнга — но там никакого RSK как раз нет, другое есть: https://www.mathnet.ru/rus/mp823
их оказывается столько же, сколько матриц из целых неотрицательных чисел, если число в клетке (i, j) считать с весом i+j-1 (так что, например, производящая функция для всех трехмерных диаграмм равна Π(1-q^i)^{-i})
это может показаться смутно гармоничным (если в плоском разбиении на клетке (i,j) лежит кубик, то и на клетках (i',j) и (i,j') при всех i'<i и j'<j лежат кубики… и всего таких кубиков минимум i+j-1…), но если пытаться придумать конкретную биекцию, возникает ощущение магии
это тоже магия соответствия RSK
выше была версия RSK, переводящая перестановку в пару стандартных таблиц одинаковой формы… здесь используется версия, переводящая произвольную матрицу из целых неотрицательных чисел в пару полустандартных таблиц одинаковой формы — а если рассечь трехмерную диаграмму Юнга по диагонали то как раз получится обычная диаграмма Юнга, в клетки которой можно записать, сколько кубкиков растет в одну сторону, а можно — сколько в другую
реализация — в комментариях
дальше решил попросить chatgpt сделать веб-версию с рисованием кубиков — и это была прямо суперразочаровывающая трата времени (все делает неправильно, не способен реагировать на замечания, да еще при доработке рисования кубиков все время норовит удалить собственно RSK)
плюнул и за 10 минут написал matplotlib-рисование кубиков (результат на картинке)… ну может еще и сделаю веб-версию, не знаю
***
у нас с Мишей Берштейном есть текст в МатПросвещении, где рассказывается в том числе про подсчет трехмерных диаграмм Юнга — но там никакого RSK как раз нет, другое есть: https://www.mathnet.ru/rus/mp823
👍5🔥3
Матпраздник прошел, попробуем вернуться к компьютерным развлечениям
сколькими способами число N можно представить в виде суммы?
(разбиения 1+2 и 2+1 и т.п. считаются одинаковыми)
начать эксперименты можно и с примитивного перебора — например, такого:
(упражнение: внесите минимальное исправление в код, чтобы перечислялись разбиения на различные слагаемые)
можно посмотреть на количества таких разбиений для разных N — на картинке Женя Смирнов с ассистентами использует умный способ это считать — а вот, наоборот, предельно прямолинейный (только всё же заменим рекурсию на динамику, чтобы работало и для относительно больших N):
получаются какие-то числа… что дальше с ними делать? как обсуждалось выше, полезно бывает посмотреть на график — и, так как p(N) быстро растет, лучше смотреть на график log p(N)
картинки (и еще пара слов) в комментариях
дальше мб будет что-то про p(N) по разным модулям
сколькими способами число N можно представить в виде суммы?
(разбиения 1+2 и 2+1 и т.п. считаются одинаковыми)
начать эксперименты можно и с примитивного перебора — например, такого:
def partitions(n,l=None):
# все разбиения числа n
# (на числа не превосходяшие l)
if l is None: l=n
if n==0: yield []
if n>0:
for i in range(l,0,-1):
# рекурсивный перебор по максимальному элементу
yield from map(lambda partition: [i]+partition,
partitions(n-i,i))
(упражнение: внесите минимальное исправление в код, чтобы перечислялись разбиения на различные слагаемые)
можно посмотреть на количества таких разбиений для разных N — на картинке Женя Смирнов с ассистентами использует умный способ это считать — а вот, наоборот, предельно прямолинейный (только всё же заменим рекурсию на динамику, чтобы работало и для относительно больших N):
def count_partitions_upto(N):
partitions = [[0 for _ in range(N+1)] for _ in range(N+1)]
for l in range(N+1):
partitions[0][l] = 1
for n in range(1,N+1):
for l in range(1,N+1):
for i in range(1,l+1):
partitions[n][l] += partitions[n-i][i]
return partitions
получаются какие-то числа… что дальше с ними делать? как обсуждалось выше, полезно бывает посмотреть на график — и, так как p(N) быстро растет, лучше смотреть на график log p(N)
картинки (и еще пара слов) в комментариях
дальше мб будет что-то про p(N) по разным модулям
👍5❤3🔥1
в дополнение к предыдущему — количества p(n) разбиений — по разным модулям
ну… заметить кое-что можно, но не так-то просто (в частности, если кто-то надеялся на периодичность — то увы)
спойлер:
p(5n+4) делится на 5
p(7n+5) делится на 7
p(11n+6) делится на 11
насколько понимаю, аналогичного утверждения mod 3 просто нет — но мб читатели меня поправят
в качестве мат. контекста можно прочитать короткую заметку Ramanujan’s congruences and Dyson’s crank (G.Andrews, K.Ono)
***
в экселе делать такую табличку даже приятнее чем в питоне
правда думал заодно и саму p(n) в экселе посчитать — но пару раз запутался в формулах и бросил (тут, конечно, с питоном намного проще) — и числа p(n) в таблицу скопировал готовые
***
заодно решил посмотреть на количества разбиений с разными рангами (контекст e.g. в заметке выше) — вот код для этого:
ну… заметить кое-что можно, но не так-то просто (в частности, если кто-то надеялся на периодичность — то увы)
спойлер:
p(7n+5) делится на 7
p(11n+6) делится на 11
насколько понимаю, аналогичного утверждения mod 3 просто нет — но мб читатели меня поправят
в качестве мат. контекста можно прочитать короткую заметку Ramanujan’s congruences and Dyson’s crank (G.Andrews, K.Ono)
***
в экселе делать такую табличку даже приятнее чем в питоне
правда думал заодно и саму p(n) в экселе посчитать — но пару раз запутался в формулах и бросил (тут, конечно, с питоном намного проще) — и числа p(n) в таблицу скопировал готовые
***
заодно решил посмотреть на количества разбиений с разными рангами (контекст e.g. в заметке выше) — вот код для этого:
def partitions_upto(N):
partitions = [[] for _ in range(N+1)]
partitions[0] = [(".",0,0)]
for n in range(1,N+1):
for i in range(n,0,-1):
for pstr,pmax,plen in partitions[n-i]:
if i>=pmax:
partitions[n].append((str(i) if pstr=="." else f"{str(i)}+{pstr}", i, plen+1))
return partitions
mod = 7
k = 4
partitions = partitions_upto(mod*k)
print(f"mod = {mod}")
for n in range(mod*k+1):
ans = [0 for _ in range(mod)]
for pstr,pmax,plen in partitions[n]:
ans[(pmax-plen) % mod] += 1
print(f"{n} — {len(partitions[n])} ({len(partitions[n]) % mod}):", *ans)
🤔1
о том, как (не) стоит считать π, и о магии им. Эйлера
1.
одна из первых идей, приходящих в голову человеку, изучавшему базовый анализ — разложить подходящую функцию в степенной ряд и что-то в него подставить
если взять arctg(x) = x - x³/3 + x⁵/5 - …, подставить¹ x=1, то получается замечательно простая формула Лейбница π/4 = 1 - 1/3 + 1/5 - 1/7 + … — чего еще желать?..
¹ и проговорить нужные слова, потому что мы оказывается, вообще-то, не внутри, а на границе круга сходимости
в прошлый раз для сотни правильных знаков хватило 4 итераций, сейчас попробуем взять… ну, скажем, 1000 членов:
видно, что погрешность ~1/1000… и вообще, можно понять, что для N слагаемых такой способ дает погрешность ~1/N — то есть чтобы получить 100 знаков нам нужно сложить ~10^(100) слагаемых (!!!)
2.
кажется, что это совсем тупиковая ветвь… и все же, не будем унывать сразу
посмотрим, скажем, на сумму 5 млн членов
погрешность получается ожидаемая, порядка 1/N, т.е. шесть цифр после запятой верны, а седьмая уже нет (получается 3,1415924… вместо 3,1415926…)
но то, что видно дальше, иначе как магией не назовешь: например, следующая дюжина цифр снова правильная!
вот что получается в результате суммирования (неправильные цифры подчеркнуты):
3.14159245358979323846464338327950278419716939938730582097494
и, на самом деле, такого количества слагаемых уже достаточно, чтобы найти не только первые 6, но и первые 60 знаков π
продолжение ниже
1.
одна из первых идей, приходящих в голову человеку, изучавшему базовый анализ — разложить подходящую функцию в степенной ряд и что-то в него подставить
если взять arctg(x) = x - x³/3 + x⁵/5 - …, подставить¹ x=1, то получается замечательно простая формула Лейбница π/4 = 1 - 1/3 + 1/5 - 1/7 + … — чего еще желать?..
¹ и проговорить нужные слова, потому что мы оказывается, вообще-то, не внутри, а на границе круга сходимости
в прошлый раз для сотни правильных знаков хватило 4 итераций, сейчас попробуем взять… ну, скажем, 1000 членов:
from mpmath import *
n = 1000
mypi = mpf(0)
s = mpf(4)
for k in range(n):
mypi += s / mpf(2*k+1)
s = -s
print(n,nstr(mypi,10),
"diff:",nstr(pi-mypi,3,min_fixed=1))
1000 3.140592654 diff: 1.0e-3
видно, что погрешность ~1/1000… и вообще, можно понять, что для N слагаемых такой способ дает погрешность ~1/N — то есть чтобы получить 100 знаков нам нужно сложить ~10^(100) слагаемых (!!!)
2.
кажется, что это совсем тупиковая ветвь… и все же, не будем унывать сразу
посмотрим, скажем, на сумму 5 млн членов
погрешность получается ожидаемая, порядка 1/N, т.е. шесть цифр после запятой верны, а седьмая уже нет (получается 3,1415924… вместо 3,1415926…)
но то, что видно дальше, иначе как магией не назовешь: например, следующая дюжина цифр снова правильная!
from mpmath import *
mp.dps = 100
n = 2500000
mypi = mpf(0)
for k in range(1,n+1):
mypi += mpf(8) / ((4*k-3)*(4*k-1))
for (s1,s2) in zip(nstr(mypi,60),nstr(pi,60)):
print(s1 if s1==s2 else s1+'\u0332',end='')
print()
вот что получается в результате суммирования (неправильные цифры подчеркнуты):
3.14159245358979323846464338327950278419716939938730582097494
и, на самом деле, такого количества слагаемых уже достаточно, чтобы найти не только первые 6, но и первые 60 знаков π
продолжение ниже
😱12👍6👌2
продолжаем суммировать ряды, или заменяем грубую силу на ___
пусть мы хотим посчитать сумму ряда, альтернативной формулы для которой сходу не видно
скажем, сумму обратных кубов (в отличие от суммы обратных квадратов или четвертых степеней она [гипотетически] не выражается через пи)
просуммируем первые N членов… насколько мы далеки от правильного ответа? сумма оставшихся членов примерно равна интегралу 1/x³ от N до ∞, т.е. ~1/2N²
то есть даже для N=100500 мы получаем всего 10 правильных цифр, а до 100 правильных цифр дойти практически невозможно (требуется ~10^{50} слагаемых)…
…но подождите! «ваш прогноз выполняется с вероятностью 40%? так говорите все наоборот, и будет выполняться с вероятностью 60%» — раз мы знаем, насколько наш ответ далек от правильного, так давайте соответствующим образом скорректируем ответ!
и действительно, для N=100500 сумма первых N членов +1/2N² дает на 5 больше правильных цифр
можно ли оценить сумму (в данном случае, хвост ряда) точнее, чем просто интегралом? оценка «интеграл ≈ сумма» возникает при приближении площади под графиком площадью столбиков — а ясно, что лучше заменить прямоугольники трапециями
если вдуматься, это учит, что точность повысится, если вычесть половину N-го члена
на самом деле, +1/2N²-1/2N³ — это начало серии поправок, а возникающие коэффициенты — это (примерно) числа Бернулли… писал про этот сюжет (формулу Эйлера-Маклорена и числа Б.) в статье «Алгебра, геометрия и анализ сумм степеней последовательных чисел», https://www.mathnet.ru/rus/mp882
***
посмотрим, как это работает на практике
возьмем, скажем, 57 поправочных членов… а сумму не обязательно даже считать до N=100500, ограничимся N=500 — и уже этого хватает для 100 правильных цифр после запятой!
***
так что, может вообще зафиксировать N, а только увеличивать количество поправочных членов (аргумент m функции improve)? степени N экспоненциально убывают, ну какие-то коэффициенты стоят при них…
проблема в том, что если начало последовательности Бернулли выглядит безобидно (1, -1/2, 1/6, -1/30…), то дальше эти числа начинают быстро — почти как факториалы! — расти (и для m=57 появляются коэффициенты ~10^{30})
ситуация достаточно тонкая: какое бы (конечное) число поправочных членов мы ни написали, при достаточно больших N они увеличивают точность вычисления — но если, наоборот, зафиксировать N, то ряд из поправочных членов расходится (в частности, с какого-то момента добавление новых поправочных членов ухудшает ситуацию!)
***
в прошлый раз речь шла о версии того же для знакопеременных рядов — и там коэффициенты поправок получались не просто рациональными, а целыми — и их можно прямо увидеть в подчеркнутых цифрах
про это поведение ряда Лейбница — взял из книжки «Mathematics by Experiment» (Borwein, Bailey) — и книжку вообще, и конкретно это место в ней мне показал Сережа Маркелов
а сама математика восходит к Эйлеру — которому очень хотелось посчитать 20 знаков суммы обратных квадратов, не складывая 10^{20} чисел
(после этого Эйлер нашел и точное значение этой суммы… а также ζ(2n), ζ(-k), и даже функциональное уравнение для ζ(x) — видимо поэтому ζ(x) теперь называют дзета-функцией… Римана)
пусть мы хотим посчитать сумму ряда, альтернативной формулы для которой сходу не видно
скажем, сумму обратных кубов (в отличие от суммы обратных квадратов или четвертых степеней она [гипотетически] не выражается через пи)
просуммируем первые N членов… насколько мы далеки от правильного ответа? сумма оставшихся членов примерно равна интегралу 1/x³ от N до ∞, т.е. ~1/2N²
то есть даже для N=100500 мы получаем всего 10 правильных цифр, а до 100 правильных цифр дойти практически невозможно (требуется ~10^{50} слагаемых)…
…но подождите! «ваш прогноз выполняется с вероятностью 40%? так говорите все наоборот, и будет выполняться с вероятностью 60%» — раз мы знаем, насколько наш ответ далек от правильного, так давайте соответствующим образом скорректируем ответ!
и действительно, для N=100500 сумма первых N членов +1/2N² дает на 5 больше правильных цифр
можно ли оценить сумму (в данном случае, хвост ряда) точнее, чем просто интегралом? оценка «интеграл ≈ сумма» возникает при приближении площади под графиком площадью столбиков — а ясно, что лучше заменить прямоугольники трапециями
если вдуматься, это учит, что точность повысится, если вычесть половину N-го члена
на самом деле, +1/2N²-1/2N³ — это начало серии поправок, а возникающие коэффициенты — это (примерно) числа Бернулли… писал про этот сюжет (формулу Эйлера-Маклорена и числа Б.) в статье «Алгебра, геометрия и анализ сумм степеней последовательных чисел», https://www.mathnet.ru/rus/mp882
***
посмотрим, как это работает на практике
возьмем, скажем, 57 поправочных членов… а сумму не обязательно даже считать до N=100500, ограничимся N=500 — и уже этого хватает для 100 правильных цифр после запятой!
from mpmath import *
mp.dps = 102
from textwrap import wrap
def bernoulli_upto(m):
ans = [mpf(1)]
for k in range(1,m+1):
b = mpf(0)
for i in range(k):
b -= ans[i]*binomial(k+1,i) / (k+1)
ans.append(chop(b,tol=1e-10))
return ans
def improve(pre,N,m):
bernoulli = bernoulli_upto(m-1)
for k in range(1,len(bernoulli)+1):
pre += (bernoulli[k-1]*k) / (2*N**(k+1))
return pre
def partial_sum(N):
ans = mpf(0)
for k in range(1,N+1):
ans += mpf(1) / k**3
return ans
def mprint(num,prec):
intp, frcp = nstr(num,prec).split(".")
print(f"{intp},",*wrap(frcp,width=5))
#N = 100500
#ans = partial_sum(N)
#mprint(ans,21) # всего 10 правильных цифр
N = 500
ans = partial_sum(N)
mprint(improve(ans,N,57),101) # все 100 цифр правильные!
***
так что, может вообще зафиксировать N, а только увеличивать количество поправочных членов (аргумент m функции improve)? степени N экспоненциально убывают, ну какие-то коэффициенты стоят при них…
проблема в том, что если начало последовательности Бернулли выглядит безобидно (1, -1/2, 1/6, -1/30…), то дальше эти числа начинают быстро — почти как факториалы! — расти (и для m=57 появляются коэффициенты ~10^{30})
ситуация достаточно тонкая: какое бы (конечное) число поправочных членов мы ни написали, при достаточно больших N они увеличивают точность вычисления — но если, наоборот, зафиксировать N, то ряд из поправочных членов расходится (в частности, с какого-то момента добавление новых поправочных членов ухудшает ситуацию!)
***
в прошлый раз речь шла о версии того же для знакопеременных рядов — и там коэффициенты поправок получались не просто рациональными, а целыми — и их можно прямо увидеть в подчеркнутых цифрах
про это поведение ряда Лейбница — взял из книжки «Mathematics by Experiment» (Borwein, Bailey) — и книжку вообще, и конкретно это место в ней мне показал Сережа Маркелов
а сама математика восходит к Эйлеру — которому очень хотелось посчитать 20 знаков суммы обратных квадратов, не складывая 10^{20} чисел
(после этого Эйлер нашел и точное значение этой суммы… а также ζ(2n), ζ(-k), и даже функциональное уравнение для ζ(x) — видимо поэтому ζ(x) теперь называют дзета-функцией… Римана)
👍13❤3🔥2