#геом_разминка #easy #8
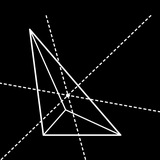
Задача. Пусть 𝐷 и 𝐸 точки на стороне 𝐵𝐶 треугольника 𝐴𝐵𝐶. Прямые через 𝐷 и 𝐸, параллельные 𝐴𝐶 и 𝐴𝐵 соответственно, пересекают 𝐴𝐵 и 𝐴𝐶 в точках 𝐹 и 𝐺. Пусть 𝑃 и 𝑄 – точки пересечения 𝐹𝐺 с описанной окружностью△𝐴𝐵𝐶. Докажите, что 𝐷𝐸𝑃𝑄 – вписанный.
Задача. Пусть 𝐷 и 𝐸 точки на стороне 𝐵𝐶 треугольника 𝐴𝐵𝐶. Прямые через 𝐷 и 𝐸, параллельные 𝐴𝐶 и 𝐴𝐵 соответственно, пересекают 𝐴𝐵 и 𝐴𝐶 в точках 𝐹 и 𝐺. Пусть 𝑃 и 𝑄 – точки пересечения 𝐹𝐺 с описанной окружностью△𝐴𝐵𝐶. Докажите, что 𝐷𝐸𝑃𝑄 – вписанный.
❤11🔥3👍1
#геом_разминка #medium #8
Задача. Пусть 𝐾, 𝐿, 𝑀, 𝑁 середины сторон 𝐴𝐵, 𝐵𝐶, 𝐶𝐷, 𝐷𝐴 соответственно вписанного четырехугольника 𝐴𝐵𝐶𝐷. Докажите, что ортоцентры треугольников 𝐴𝐾𝑁, 𝐵𝐾𝐿, 𝐶𝐿𝑀, 𝐷𝑀𝑁 являются вершинами параллелограмма.
Задача. Пусть 𝐾, 𝐿, 𝑀, 𝑁 середины сторон 𝐴𝐵, 𝐵𝐶, 𝐶𝐷, 𝐷𝐴 соответственно вписанного четырехугольника 𝐴𝐵𝐶𝐷. Докажите, что ортоцентры треугольников 𝐴𝐾𝑁, 𝐵𝐾𝐿, 𝐶𝐿𝑀, 𝐷𝑀𝑁 являются вершинами параллелограмма.
❤🔥10❤5🔥3✍1
#геом_разминка #medium #10
Задача. Дан выпуклый четырёхугольник 𝐴𝐵𝐶𝐷. Пусть 𝑃 и 𝑄 — точки пересечения лучей 𝐵𝐴 и 𝐶𝐷, 𝐵𝐶 и 𝐴𝐷 соответственно, а 𝐻 — проекция 𝐷 на 𝑃𝑄. Докажите, что четырёхугольник 𝐴𝐵𝐶𝐷 является описанным тогда и только тогда, когда вписанные окружности треугольников 𝐴𝐷𝑃 и 𝐶𝐷𝑄 видны из точки 𝐻 под равными углами.
Задача. Дан выпуклый четырёхугольник 𝐴𝐵𝐶𝐷. Пусть 𝑃 и 𝑄 — точки пересечения лучей 𝐵𝐴 и 𝐶𝐷, 𝐵𝐶 и 𝐴𝐷 соответственно, а 𝐻 — проекция 𝐷 на 𝑃𝑄. Докажите, что четырёхугольник 𝐴𝐵𝐶𝐷 является описанным тогда и только тогда, когда вписанные окружности треугольников 𝐴𝐷𝑃 и 𝐶𝐷𝑄 видны из точки 𝐻 под равными углами.
❤12🔥3⚡2🥰2😍2
#по_факту
Мы побывали в древнем городе Перге 🏛, где родился Аполлоний. Он исследовал задачу о пучках окружностей, которые позднее были названы в честь него.
Окружность Аполлония — ГМТ точек 𝑃 таких, что отношение расстояний 𝐴𝑃/𝑃𝐵 до двух фиксированных точек 𝐴 и 𝐵 равно некоторой константе.
С треугольником 𝐴𝐵𝐶 связывают три окружности Аполлония — по одной для каждой из его вершин: 𝐴-окружностью Аполлония называют ГМТ таких точек 𝑃, что отношение 𝐵𝑃/𝑃𝐶 равно 𝐵𝐴/𝐴𝐶.
Факт. Окружности Аполлония треугольника имеет общую радикальную ось.
P.S. Кстати, этот пост — подсказка к вчерашней разминке.
Мы побывали в древнем городе Перге 🏛, где родился Аполлоний. Он исследовал задачу о пучках окружностей, которые позднее были названы в честь него.
Окружность Аполлония — ГМТ точек 𝑃 таких, что отношение расстояний 𝐴𝑃/𝑃𝐵 до двух фиксированных точек 𝐴 и 𝐵 равно некоторой константе.
С треугольником 𝐴𝐵𝐶 связывают три окружности Аполлония — по одной для каждой из его вершин: 𝐴-окружностью Аполлония называют ГМТ таких точек 𝑃, что отношение 𝐵𝑃/𝑃𝐶 равно 𝐵𝐴/𝐴𝐶.
Факт. Окружности Аполлония треугольника имеет общую радикальную ось.
P.S. Кстати, этот пост — подсказка к вчерашней разминке.
❤🔥15❤8🔥6
#геом_разминка #medium #9 #не_баян_а_классика
Задача. Пусть 𝐴 — одна из двух различных точек пересечения двух неравных окружностей 𝜔₁ и 𝜔₂ с центрами 𝑂₁ и 𝑂₂ соответственно. Одна из общих касательных к окружностям касается 𝜔₁ в точке 𝑃₁ и 𝜔₂ в точке 𝑃₂, а другая касается 𝜔₁ в точке 𝑄₁ и 𝜔₂ в точке 𝑄₂. Пусть 𝑀₁ — середина отрезка 𝑃₁𝑄₁, а 𝑀₂ — середина отрезка 𝑃₂𝑄₂. Докажите, что ∠𝑂₁𝐴𝑂₂ = ∠𝑀₁𝐴𝑀₂.
Задача. Пусть 𝐴 — одна из двух различных точек пересечения двух неравных окружностей 𝜔₁ и 𝜔₂ с центрами 𝑂₁ и 𝑂₂ соответственно. Одна из общих касательных к окружностям касается 𝜔₁ в точке 𝑃₁ и 𝜔₂ в точке 𝑃₂, а другая касается 𝜔₁ в точке 𝑄₁ и 𝜔₂ в точке 𝑄₂. Пусть 𝑀₁ — середина отрезка 𝑃₁𝑄₁, а 𝑀₂ — середина отрезка 𝑃₂𝑄₂. Докажите, что ∠𝑂₁𝐴𝑂₂ = ∠𝑀₁𝐴𝑀₂.
❤10❤🔥2🔥2
Новогодняя #геом_разминка #hard #10
Задача. Даны четыре попарно непересекающиеся окружности 𝛾₁, 𝛾₂, 𝛾₃ и 𝛾₄. Известно, что существует окружность 𝜔, которая касается как обеих общих внешних касательных к 𝛾₁ и 𝛾₃, так и обеих общих внешних касательных к 𝛾₂ и 𝛾₄. Докажите, что существует окружность, которая касается как обеих общих внешних касательных к 𝛾₁ и 𝛾₂, так и обеих общих внешних касательных к 𝛾₃ и 𝛾₄.
Всех с наступающим 🎄
Задача. Даны четыре попарно непересекающиеся окружности 𝛾₁, 𝛾₂, 𝛾₃ и 𝛾₄. Известно, что существует окружность 𝜔, которая касается как обеих общих внешних касательных к 𝛾₁ и 𝛾₃, так и обеих общих внешних касательных к 𝛾₂ и 𝛾₄. Докажите, что существует окружность, которая касается как обеих общих внешних касательных к 𝛾₁ и 𝛾₂, так и обеих общих внешних касательных к 𝛾₃ и 𝛾₄.
Всех с наступающим 🎄
🎄29❤7🥰4❤🔥2😍1
В последние минуты 🕰 уходящего года мы вспоминаем яркие, эмоциональные и теплые моменты🎄
2025 год был богат красивыми геомами. По традиции мы составили свой список задач, запомнившихся нам. Последнее место в этом списке пустует — его мы оставили для задачи, которую мы забыли, а вспомните вы. Пишите понравившиеся вам задачи в комментах👇
Желаем больше новых открытий и творческих успехов, а мы будем радовать вас, как и прежде, красивыми задачами!
С Новым2️⃣ 0️⃣ 2️⃣ 6️⃣ годом!
2025 год был богат красивыми геомами. По традиции мы составили свой список задач, запомнившихся нам. Последнее место в этом списке пустует — его мы оставили для задачи, которую мы забыли, а вспомните вы. Пишите понравившиеся вам задачи в комментах
Желаем больше новых открытий и творческих успехов, а мы будем радовать вас, как и прежде, красивыми задачами!
С Новым
Please open Telegram to view this post
VIEW IN TELEGRAM
❤22🎅3☃2🎄2
#геом_разминка #medium #9
Продолжаем серию прошлогодних постов: снова задачка про описанный четырехугольник.
Задача. Даны касающиеся в точке 𝑃 окружности Ω и 𝜔. На 𝜔 взята произвольная точка 𝑄, на луче 𝑃𝑄 выбрана точка 𝑅 так, что из нее можно провести две касательные 𝑠 и 𝑛 к окружности 𝜔. Пусть 𝑜 и 𝑤 — касательные из точки 𝑄 к окружности Ω. Докажите, что существует окружность, касающаяся прямых 𝑠, 𝑛, 𝑜, 𝑤.
С Новым годом ☃️
Продолжаем серию прошлогодних постов: снова задачка про описанный четырехугольник.
Задача. Даны касающиеся в точке 𝑃 окружности Ω и 𝜔. На 𝜔 взята произвольная точка 𝑄, на луче 𝑃𝑄 выбрана точка 𝑅 так, что из нее можно провести две касательные 𝑠 и 𝑛 к окружности 𝜔. Пусть 𝑜 и 𝑤 — касательные из точки 𝑄 к окружности Ω. Докажите, что существует окружность, касающаяся прямых 𝑠, 𝑛, 𝑜, 𝑤.
С Новым годом ☃️
❤12❤🔥4☃4🎅1
#геом_разминка #medium #9
Задача. Окружность 𝜔 вписана в квадрат 𝐾𝐿𝑀𝑁. Отрезок 𝐴𝐵 является диаметром 𝜔, причём 𝐴 и 𝐵 — середины противоположных сторон квадрата 𝐾𝐿𝑀𝑁. Две окружности Г₁ и Г₂ имеют центры на прямой 𝐴𝐵, касаются друг друга внешним образом, и каждая из них касается окружности 𝜔 внутренним образом. Две окружности Г₃ и Г₄ касаются Г₁ и Г₂ внешним образом и касаются 𝜔 внутренним образом. С помощью циркуля и линейки постройте общую касательную к окружностям Г₁ и Г₃, минимизируя использование циркуля.
Какое минимальное число действий циркулем требуется для этого построения?
Задача. Окружность 𝜔 вписана в квадрат 𝐾𝐿𝑀𝑁. Отрезок 𝐴𝐵 является диаметром 𝜔, причём 𝐴 и 𝐵 — середины противоположных сторон квадрата 𝐾𝐿𝑀𝑁. Две окружности Г₁ и Г₂ имеют центры на прямой 𝐴𝐵, касаются друг друга внешним образом, и каждая из них касается окружности 𝜔 внутренним образом. Две окружности Г₃ и Г₄ касаются Г₁ и Г₂ внешним образом и касаются 𝜔 внутренним образом. С помощью циркуля и линейки постройте общую касательную к окружностям Г₁ и Г₃, минимизируя использование циркуля.
Какое минимальное число действий циркулем требуется для этого построения?
🥰7❤4❤🔥3
#геом_разминка #easy #8
Задача. Пусть 𝑃 — произвольная точка на диагонали 𝐵𝐷 прямоугольника 𝐴𝐵𝐶𝐷, 𝐹 — проекция точки 𝑃 на сторону 𝐵𝐶. Точка 𝐻 взята на отрезке 𝐵𝐶 так, что 𝐵𝐹 = 𝐹𝐻. Отрезки 𝑃𝐶 и 𝐴𝐻 пересекаются в точке 𝑄. Докажите, что площади треугольников 𝐴𝑃𝑄 и 𝐶𝐻𝑄 равны.
Задача. Пусть 𝑃 — произвольная точка на диагонали 𝐵𝐷 прямоугольника 𝐴𝐵𝐶𝐷, 𝐹 — проекция точки 𝑃 на сторону 𝐵𝐶. Точка 𝐻 взята на отрезке 𝐵𝐶 так, что 𝐵𝐹 = 𝐹𝐻. Отрезки 𝑃𝐶 и 𝐴𝐻 пересекаются в точке 𝑄. Докажите, что площади треугольников 𝐴𝑃𝑄 и 𝐶𝐻𝑄 равны.
❤8❤🔥5🔥3
#геом_разминка #medium #8
Задача. В треугольнике 𝐴𝐵𝐶 верно, что ∠𝐶 = 2∠𝐵. Внутри треугольника 𝐴𝐵𝐶 взята точка 𝐹 так, что 𝐴𝑃 = 𝐴𝐶 и 𝑃𝐵 = 𝑃𝐶. Докажите, что 𝐴𝑃 делит угол ∠𝐴𝐵𝐶 на три равные части.
Задача. В треугольнике 𝐴𝐵𝐶 верно, что ∠𝐶 = 2∠𝐵. Внутри треугольника 𝐴𝐵𝐶 взята точка 𝐹 так, что 𝐴𝑃 = 𝐴𝐶 и 𝑃𝐵 = 𝑃𝐶. Докажите, что 𝐴𝑃 делит угол ∠𝐴𝐵𝐶 на три равные части.
❤9❤🔥5🔥3👍1
#геом_разминка #hard #9
Задача. Вписанная окружность четырехугольника 𝐴𝐵𝐶𝐷 касается сторон 𝐷𝐴, 𝐴𝐵, 𝐵𝐶, 𝐶𝐷 в точках 𝐾, 𝐿, 𝑀, 𝑁 соответственно. Пусть 𝛼, 𝛽, 𝛾, 𝛿 — вписанные окружности треугольников 𝐴𝐾𝐿, 𝐵𝐿𝑀, 𝐶𝑀𝑁, 𝐷𝐾𝑁 соответственно. Пусть 𝑝, 𝑞, 𝑟, 𝑠 — общие внешние касательные к парам 𝛼 и 𝛽, 𝛽 и 𝛾, 𝛾 и 𝛿, 𝛿 и 𝛼, отличные от сторон четырехугольника 𝐴𝐵𝐶𝐷. Докажите, что 𝑝, 𝑞, 𝑟, 𝑠 образуют ромб.
Задача. Вписанная окружность четырехугольника 𝐴𝐵𝐶𝐷 касается сторон 𝐷𝐴, 𝐴𝐵, 𝐵𝐶, 𝐶𝐷 в точках 𝐾, 𝐿, 𝑀, 𝑁 соответственно. Пусть 𝛼, 𝛽, 𝛾, 𝛿 — вписанные окружности треугольников 𝐴𝐾𝐿, 𝐵𝐿𝑀, 𝐶𝑀𝑁, 𝐷𝐾𝑁 соответственно. Пусть 𝑝, 𝑞, 𝑟, 𝑠 — общие внешние касательные к парам 𝛼 и 𝛽, 𝛽 и 𝛾, 𝛾 и 𝛿, 𝛿 и 𝛼, отличные от сторон четырехугольника 𝐴𝐵𝐶𝐷. Докажите, что 𝑝, 𝑞, 𝑟, 𝑠 образуют ромб.
🔥17❤9❤🔥4🤯1
#геом_разминка #medium #9
Задача. Дан выпуклый четырехугольник 𝐴𝐵𝐶𝐷, в котором 𝐴𝐵 = 𝐴𝐷. На диагонали 𝐴𝐶 выбрана точка 𝑇 так, что ∠𝐴𝐵𝑇 + ∠𝐴𝐷𝑇 = ∠𝐵𝐶𝐷. Докажите, что 𝐶𝑇 ⩾ 2(𝐴𝐵 − 𝐴𝑇).
Задача. Дан выпуклый четырехугольник 𝐴𝐵𝐶𝐷, в котором 𝐴𝐵 = 𝐴𝐷. На диагонали 𝐴𝐶 выбрана точка 𝑇 так, что ∠𝐴𝐵𝑇 + ∠𝐴𝐷𝑇 = ∠𝐵𝐶𝐷. Докажите, что 𝐶𝑇 ⩾ 2(𝐴𝐵 − 𝐴𝑇).
❤9🔥2🥰1
#геом_разминка #medium #8
Задача. На рисунке в нижнем ряду изображены 5 равнобедренных треугольников с длинами оснований 12, 13, 14, 15, 16 см. В рядах выше изображены 10 четырехугольников. Каждый четырехугольник представляет собой ромб, а вершина башни — квадрат. Какова площадь квадрата?
Задача. На рисунке в нижнем ряду изображены 5 равнобедренных треугольников с длинами оснований 12, 13, 14, 15, 16 см. В рядах выше изображены 10 четырехугольников. Каждый четырехугольник представляет собой ромб, а вершина башни — квадрат. Какова площадь квадрата?
🔥24❤7🥰4👎1
#геом_разминка #medium #9
Задача. Дан треугольник 𝐴𝐵𝐶, вписанная окружность которого с центром в 𝐼 касается сторон 𝐵𝐶, 𝐶𝐴, 𝐴𝐵 в точках 𝐷, 𝐸, 𝐹 соответственно. Прямая, проходящая через точку 𝐴 и параллельная отрезку 𝐸𝐹, пересекает прямую 𝐷𝐸 в точке 𝑃. Докажите, что прямая, проходящая через точку 𝐶 и перпендикулярная отрезку 𝐼𝑃, делит отрезок 𝐸𝐹 пополам.
Задача. Дан треугольник 𝐴𝐵𝐶, вписанная окружность которого с центром в 𝐼 касается сторон 𝐵𝐶, 𝐶𝐴, 𝐴𝐵 в точках 𝐷, 𝐸, 𝐹 соответственно. Прямая, проходящая через точку 𝐴 и параллельная отрезку 𝐸𝐹, пересекает прямую 𝐷𝐸 в точке 𝑃. Докажите, что прямая, проходящая через точку 𝐶 и перпендикулярная отрезку 𝐼𝑃, делит отрезок 𝐸𝐹 пополам.
❤6❤🔥5🥰2👍1
#геом_разминка #medium #7
Задача. Три квадрата 𝐴𝐾𝐿𝐹, 𝐵𝐶𝑁𝐾, 𝐷𝐸𝐿𝑁 расположены так, что между ними образован треугольник 𝐾𝐿𝑁 (нумерация вершин квадратов и треугольника против часовой стрелки). Площади квадратов соответственно равны 5 см², 10 см² и 13 см². Найдите площадь шестиугольника 𝐴𝐵𝐶𝐷𝐸𝐹.
Задача. Три квадрата 𝐴𝐾𝐿𝐹, 𝐵𝐶𝑁𝐾, 𝐷𝐸𝐿𝑁 расположены так, что между ними образован треугольник 𝐾𝐿𝑁 (нумерация вершин квадратов и треугольника против часовой стрелки). Площади квадратов соответственно равны 5 см², 10 см² и 13 см². Найдите площадь шестиугольника 𝐴𝐵𝐶𝐷𝐸𝐹.
❤6🔥5❤🔥2
#геом_разминка #medium #9
Задача. Точки 𝐻 и 𝐼 — соответственно ортоцентр и центр вписанной окружности остроугольного треугольника 𝐴𝐵𝐶. Описанная окружность треугольника 𝐵𝐶𝐼 пересекает отрезок 𝐴𝐵 в точке 𝑃 (отличной от 𝐵). Точка 𝐾 — проекция точки 𝐻 на 𝐴𝐼, точка 𝑄 симметрична точке 𝑃 относительно точки 𝐾. Докажите, что точки 𝐵, 𝐻 и 𝑄 лежат на одной прямой.
Задача. Точки 𝐻 и 𝐼 — соответственно ортоцентр и центр вписанной окружности остроугольного треугольника 𝐴𝐵𝐶. Описанная окружность треугольника 𝐵𝐶𝐼 пересекает отрезок 𝐴𝐵 в точке 𝑃 (отличной от 𝐵). Точка 𝐾 — проекция точки 𝐻 на 𝐴𝐼, точка 𝑄 симметрична точке 𝑃 относительно точки 𝐾. Докажите, что точки 𝐵, 𝐻 и 𝑄 лежат на одной прямой.
🔥7❤6❤🔥3👍1
#уголки_планеты #по_факту
Редакция нашего паблика недавно побывала в аэропорту✈️ Измира 🇹🇷 Колонны аэропорта, как и Шуховские башни, сделаны в форме однополостных гиперболоидов🦄
Напомним, что в презентации вы сможете найти и другие примеры, когда поверхности второго порядка встречаются в архитектуре 🏢 Кроме того, там же есть картинка к забавному доказательству теоремы Брианшона с выходом в пространство.
Факт. У гиперболоида есть 2 семейства прямолинейных образующих. Любые 2 образующие одного семейства скрещиваются. Любые 2 образующие разных семейств пересекаются.
Как с помощью этого факта завершить доказательство теоремы Брианшона? Обсудить можно тут.
Редакция нашего паблика недавно побывала в аэропорту
Напомним, что в презентации вы сможете найти и другие примеры, когда поверхности второго порядка встречаются в архитектуре 🏢 Кроме того, там же есть картинка к забавному доказательству теоремы Брианшона с выходом в пространство.
Факт. У гиперболоида есть 2 семейства прямолинейных образующих. Любые 2 образующие одного семейства скрещиваются. Любые 2 образующие разных семейств пересекаются.
Как с помощью этого факта завершить доказательство теоремы Брианшона? Обсудить можно тут.
Please open Telegram to view this post
VIEW IN TELEGRAM
❤7❤🔥3🔥2😍2🙏1