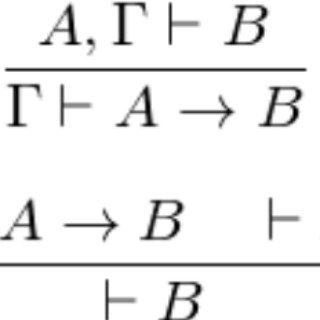An embedded DSL in Agda for Hilbert-style proofs
https://janmasrovira.gitlab.io/ascetic-slug/post/edsl-hilbert/
https://janmasrovira.gitlab.io/ascetic-slug/post/edsl-hilbert/
janmasrovira.gitlab.io
An Agda eDSL for well-typed Hilbert style proofs
I present an Agda eDSL for writing Hilbert style proofs for logic $K$.
This blog consists of two main parts. The first part presents the language and some examples. The second offers some insight into the key parts of the implementation. The latter targets…
This blog consists of two main parts. The first part presents the language and some examples. The second offers some insight into the key parts of the implementation. The latter targets…
Pure & constructive mathematics in theory and use
An embedded DSL in Agda for Hilbert-style proofs https://janmasrovira.gitlab.io/ascetic-slug/post/edsl-hilbert/
Note that the used logic is equivalent to one only using Ax 1,2,3, as long as you have a notion of assumption.
Guarded computational type theory
https://arxiv.org/abs/1804.09098
A type theory capuring the notion of productivity while being a compuational metalanguage.
[Thanks to petercommand]
https://arxiv.org/abs/1804.09098
A type theory capuring the notion of productivity while being a compuational metalanguage.
[Thanks to petercommand]
[MLTT resources]
The original notes: https://archive-pml.github.io/martin-lof/pdfs/Bibliopolis-Book-retypeset-1984.pdf
A formal overview: https://ncatlab.org/nlab/show/Martin-L%C3%B6f+dependent+type+theory
Another denoscription: http://www.cse.chalmers.se/~peterd/papers/IntuitionisticTypeTheory150505.pdf
Programming in Martin-Löf type theory: https://www.dimap.ufrn.br/~regivan/pub/Programming_In_Martin_Loef_Type_Theory.pdf
[Resources for MLTT or similar about specific languages:]
Logic and Proof in Lean: https://leanprover.github.io/logic_and_proof/
General Theorem Proving in Lean: https://leanprover.github.io/theorem_proving_in_lean/
Programming Language Foundations in Agda: https://plfa.github.io/
Software foundations (based on Coq): https://softwarefoundations.cis.upenn.edu/current/index.html
The Nuprl Proof Development System: http://www.nuprl.org/book/
[HoTT resources]
The HoTT Book: https://homotopytypetheory.org/book/
HoTT in Agda: https://github.com/HoTT/HoTT-Agda
HoTT in Coq: https://github.com/HoTT/HoTT
The CoqHoTT project: http://coqhott.gforge.inria.fr/
Cubical type theory: https://arxiv.org/abs/1611.02108
Cubical type theory as Agda extension: https://agda.readthedocs.io/en/latest/language/cubical.html
Cubical Agda library: https://github.com/agda/cubical
The main implementation: https://github.com/mortberg/cubicaltt
An introduction to cubicaltt: https://homotopytypetheory.org/2017/09/16/a-hands-on-introduction-to-cubicaltt/
The original notes: https://archive-pml.github.io/martin-lof/pdfs/Bibliopolis-Book-retypeset-1984.pdf
A formal overview: https://ncatlab.org/nlab/show/Martin-L%C3%B6f+dependent+type+theory
Another denoscription: http://www.cse.chalmers.se/~peterd/papers/IntuitionisticTypeTheory150505.pdf
Programming in Martin-Löf type theory: https://www.dimap.ufrn.br/~regivan/pub/Programming_In_Martin_Loef_Type_Theory.pdf
[Resources for MLTT or similar about specific languages:]
Logic and Proof in Lean: https://leanprover.github.io/logic_and_proof/
General Theorem Proving in Lean: https://leanprover.github.io/theorem_proving_in_lean/
Programming Language Foundations in Agda: https://plfa.github.io/
Software foundations (based on Coq): https://softwarefoundations.cis.upenn.edu/current/index.html
The Nuprl Proof Development System: http://www.nuprl.org/book/
[HoTT resources]
The HoTT Book: https://homotopytypetheory.org/book/
HoTT in Agda: https://github.com/HoTT/HoTT-Agda
HoTT in Coq: https://github.com/HoTT/HoTT
The CoqHoTT project: http://coqhott.gforge.inria.fr/
Cubical type theory: https://arxiv.org/abs/1611.02108
Cubical type theory as Agda extension: https://agda.readthedocs.io/en/latest/language/cubical.html
Cubical Agda library: https://github.com/agda/cubical
The main implementation: https://github.com/mortberg/cubicaltt
An introduction to cubicaltt: https://homotopytypetheory.org/2017/09/16/a-hands-on-introduction-to-cubicaltt/
Pure & constructive mathematics in theory and use pinned «[MLTT resources] The original notes: https://archive-pml.github.io/martin-lof/pdfs/Bibliopolis-Book-retypeset-1984.pdf A formal overview: https://ncatlab.org/nlab/show/Martin-L%C3%B6f+dependent+type+theory Another denoscription: http://www.cse.chalmers.se/~…»
A type checker for a modal dependently typed theory
https://github.com/jozefg/blott
[Thanks to clayrat]
https://github.com/jozefg/blott
[Thanks to clayrat]
GitHub
GitHub - jozefg/blott: An experimental type checker for a modal dependent type theory.
An experimental type checker for a modal dependent type theory. - jozefg/blott
A proof checker for cartesian cubical type theory
https://github.com/RedPRL/redtt
This goes even beyond the generality of cubical type theory, since paths are defined by even more general cube boundaries.
[Thanks to Brett]
https://github.com/RedPRL/redtt
This goes even beyond the generality of cubical type theory, since paths are defined by even more general cube boundaries.
[Thanks to Brett]
GitHub
GitHub - RedPRL/redtt: "Between the darkness and the dawn, a red cube rises!": a proof assistant for cartesian cubical type theory
"Between the darkness and the dawn, a red cube rises!": a proof assistant for cartesian cubical type theory - RedPRL/redtt
A formal proof of the independence of the continuum independence written in Lean
https://github.com/flypitch/flypitch
https://github.com/flypitch/flypitch
GitHub
GitHub - flypitch/flypitch: A formal proof of the independence of the continuum hypothesis
A formal proof of the independence of the continuum hypothesis - flypitch/flypitch
An introduction to category theory
http://www.cs.man.ac.uk/~hsimmons/zCATS.pdf
Note that this one seemed pretty simple and not that formal to me, compared to many others.
http://www.cs.man.ac.uk/~hsimmons/zCATS.pdf
Note that this one seemed pretty simple and not that formal to me, compared to many others.
A Unified Approach to Solving Seven Programming Problems (Functional Pearl)
http://io.livecode.ch/learn/namin/icfp2017-artifact-auas7pp
An introduction to logic- and metaprogramming using Scheme, while showing true test-driven development.
http://io.livecode.ch/learn/namin/icfp2017-artifact-auas7pp
An introduction to logic- and metaprogramming using Scheme, while showing true test-driven development.
Twelf
http://twelf.org/wiki/Main_Page
A language to specify implement and prove properties of deductive systems.
http://twelf.org/wiki/Main_Page
A language to specify implement and prove properties of deductive systems.
Asymptotically, almost all Lambda-Terms are strongly normalizing
https://arxiv.org/pdf/0903.5505.pdf
This paper shows that almost all lambda terms are strongly normalizing, while for combinatory logic, the opposite applies.
https://arxiv.org/pdf/0903.5505.pdf
This paper shows that almost all lambda terms are strongly normalizing, while for combinatory logic, the opposite applies.
To be precise, the lower bound for normalizing lambda terms of size n is ((4 - eps) * n/ln(n))^(n-(n/ln(n))), where eps is between 0 and 4.