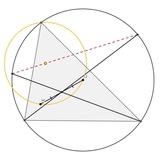
Обобщение окружности Конвея. Не мог не сделать пост про это, уж больно красиво конструкция выглядит, как по мне

Сегодня пост с красивой задачей от @egfed.

L - отражение ортоцентра АВС относительно центра описанной окружности, L' - изогональное сопряжение L. Доказать вписанность...

Красивая задача про треугольник с углом 60° от @Edinburgh_of_the_Seven_Seas.

Собственно, центры цветных окружностей - середины хорд (АВС), содержащих биссектрисы; и они касаются соотв. сторон треугольника. Доказать, что цветные окружности также касаются прямой, проходящей через середину М АС (и перп. МХ_125, но это условие можно игнорировать).

Это дополнение к этой задаче...

Нереально крутая задача от того же автора @Edinburgh_of_the_Seven_Seas.

Гипербола Джерабека треугольника АВС (ее центр - Х_125) пересекает его описанную окружность в точке D. Пусть А' - отражение А отн-о Х_125, Е - пересечение DA', BC; а P, Q - пересечения прямой EX_125 и гиперболы. Доказать, что три (!) окружности (PQO), (QHO), (PHO) касаются описанной окружности.

Upd: гипербола Джерабека проходит через вершины треугольника, ортоцентр Н и центр описанной окружности О.

Сегодня задача от @Mamonovclhgffkuffhj! Требуется доказать, что существует окружность, касающаяся красных объектов (касательной ко вписанной окружности к той точке на рисунке, касательных к полувневписанной окружности, полуописанной окружности).
Внимательные читатели геометрических каналов могут кое-что заметить...

Также желаем удачи всем участникам олимпиады Шарыгина завтра и послезавтра 😊

Итак, олимпиада Шарыгина прошла, надеюсь, что некоторые задачи многим понравились. А мы продолжаем нашу работу! Вот такой красивый факт нашел @Edinburgh_of_the_Seven_Seas.

На картинке P, P' - изогонально сопряжённые точки. Эллипс с фокусами P, P' проходит через центр гиперболы ABCPP'. Доказать, что пунктир - биссектриса.

Ладно, на самом деле в задаче выше точку O можно взять любую.

Красные точки - пересечения биссектрис противоположных углов, а зеленая - изогональное сопряжение точки пересечения диагоналей. Доказать что красный угол равен 90°.

Задача от @MeZox_111

Соответственные точки - Микели соответствующих четырехугольников как(голубая точка - голубого, зеленая точка - зеленого, красный и розовый не нарисованы)

Красиво, странно, что не баян

Мы не забыли о постах! Сегодня такая вот задача от @Mamonovclhgffkuffhj. Хотя не очень похоже с виду))))

Сегодня вот такая задачка от меня.

В треугольнике ABC с ортоцентром H точка M - середина AC. Пусть HM пересекает (ABC) в P; K' - отражение точки пересечения касательных относительно AC; M' - отражение M относительно прямой через основания высот.
Докажите, что выделенный четырёхугольник гармонический.

Давайте немного предложку почистим... У нас есть много хороших задач, которые мы вовремя случайно забыли запостить. Вот такую задачу очень давно предлагал @paleev4.

Upd: на рисунке описанный эллипс Штейнера серого треугольника.

Добренькая задача от @MeZox_111

Сегодняшнюю задачку предложил @MigelSa.

В треугольнике АВС угол С равен 60°. I - его инцентр; Ш_BIC, Ш_AIC - точки Шалтая понятно каких треугольников. доказать что центр красной окружности лежит на OI.

Иногда мы постим и добрые, и красивые задачи, например сегодня. Ее нам предложил @vlad9100.

На рисунке красная точка - центр красной окружности. Доказать, что три точки лежат на одной пунктирной прямой.

Сегодня постим шедевр от @Edinburgh_of_the_Seven_Seas.

Выделенный треугольник - ортотреугольник. О - центр описанной окружности АВС. Точка X - произвольная на окружности Эйлера АВС, окружность (XOJ) касается описанной. Все остальные точки и прямые строятся понятно как. Доказать касание.

Да, эта задача обобщается, но мне в такой оригинальной формулировке гораздо больше нравится.

Сегодня совместная задача от @BotaynaT2 и @vlad9100

Условие: Дан вписано-описанный четырехугольник, красная точка - центр описанной, синяя - вписанной.
Доказать что центр фиолетовой окружности, центр вписанной и точка пересечения противоположных сторон лежат на одной прямой.

Прикольно

факт от @emil_sadykov

(!) произведение синусов половинных углов у таких двух треугольников равны