Всем доброе утро. Нам очень понравилась идея тематических дней, так что сегодня для вас ещё один. День кубик ;) Мы постарались подобрать не классические задачи на кубики, а некоторые более неожиданные факты, так что задачи сегодня будут довольно продвинутые.


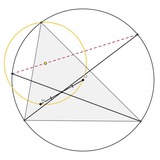
Но начнем с довольно простой задачи. Точки P и P' на рисунке изогонально сопряжены.

Итак, вторая задача уже сразу довольно интересная. Я думаю, к ней рисунок будет излишним.

Конечная точка такова, что прямая через неё и трилинейный полюс её ортотрансверсали проходит через центроид. Доказать, что эта точка лежит на гиперболе Киперта.

В качестве третьей задачи предлагаем довольно классическую задачу попроще.

Be - точка Бевена (X(40))
L - симметрия ортоцентра относительно центра описанной (X(20))

К четвертой задаче рисунок также будет излишним.

Существует ли остроугольный треугольник, в котором середина отрезка между точками Торричелли лежит вне него?

в канал добавлена новая реакция специально для постов юсуфа

Убейся

Ненавидь меня это нормально👌😂

Ну и напоследок предлагаю задачу, которую я не умею решать.

Кубику Нойберга повернули на 120° в разные стороны относительно центра описанной окружности. Докажите, что полученные три кубики лежат в одном пучке.

Тематический день кубик - ВСЁ. Заказывайте тематические дни в комментариях, м.б. мы сделаем.

Разминка №21.

Точка Н - ортоцентр большого треугольника.

Народная задача от @Edinburgh_of_the_Seven_Seas

Красиво 🤤

Разминка №22.

Одноцветные углы на рисунке в сумме дают или 90° или 180° (сумма синих углов - 90°, сумма красных углов - 90°, а сумма зелёных углов - 180°).
Синие отрезки - биссектрисы соотв. углов.

ну и народная красота от @IvanMChas

кто-то помешан на шалтаях-болтаях...

Тут произошли тех-шоколадки, и я неверно нарисовал рисунок... Перерисовывать мне лень, поэтому держите оригинальное условие. Тот, кто хочет, все-равно решит)

Разминка №23.

АА', ВВ', СС' - биссектрисы треугольника АВС. Доказать, что периметр АВС хотя бы вдвое больше периметра А'В'С'.

Вчера был выходной 😁

Upd: оба админа, которые делают рисуночки, заболели, поэтому объявляется неделя стереомы, кг и неравенств

Интернет не анонимен

Кто-то пожаловался в комментариях, что предыдущая разминка была слишком простой.
Итак, РАЗМИНКА 24.

В треугольнике АВС угол В тупой, а H и I - его ортоцентр и инцентр. Доказать, что HI не больше, чем 4S(AHC)/P(ABC).

Ну и в завершение дня предлагаем вам решить очень красивую народную задачу от @IvanMChas.

Бс, Бb - C-Болтай AFC и B-Болтай АFB.

Доброе утро! Разминка №25.

Дан выпуклый многоугольник, никакие две стороны которого не параллельны. Для каждой из его сторон рассмотрим угол, под которым она видна из вершины, наиболее удалённой от этой стороны. Доказать, что сумма всех таких углов равна 180°.

Разминка №26

Наверное моё любимое нер-во...

Внутри окружности радиуса R расположено n точек. Докажите, что сумма квадратов попарных расстояний между ними не превосходит (nR)^2.