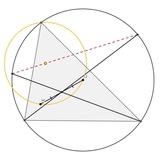
Давайте немного предложку почистим... У нас есть много хороших задач, которые мы вовремя случайно забыли запостить. Вот такую задачу очень давно предлагал @paleev4.
Upd: на рисунке описанный эллипс Штейнера серого треугольника.
Upd: на рисунке описанный эллипс Штейнера серого треугольника.
🔥4👍2🤡2❤1🗿1
Сегодняшнюю задачку предложил @MigelSa.
В треугольнике АВС угол С равен 60°. I - его инцентр; Ш_BIC, Ш_AIC - точки Шалтая понятно каких треугольников. доказать что центр красной окружности лежит на OI.
В треугольнике АВС угол С равен 60°. I - его инцентр; Ш_BIC, Ш_AIC - точки Шалтая понятно каких треугольников. доказать что центр красной окружности лежит на OI.
❤7👍1🔥1
Иногда мы постим и добрые, и красивые задачи, например сегодня. Ее нам предложил @vlad9100.
На рисунке красная точка - центр красной окружности. Доказать, что три точки лежат на одной пунктирной прямой.
На рисунке красная точка - центр красной окружности. Доказать, что три точки лежат на одной пунктирной прямой.
👍5🥰3❤2🗿1
Сегодня постим шедевр от @Edinburgh_of_the_Seven_Seas.
Выделенный треугольник - ортотреугольник. О - центр описанной окружности АВС. Точка X - произвольная на окружности Эйлера АВС, окружность (XOJ) касается описанной. Все остальные точки и прямые строятся понятно как. Доказать касание.
Да,эта задача обобщается , но мне в такой оригинальной формулировке гораздо больше нравится.
Выделенный треугольник - ортотреугольник. О - центр описанной окружности АВС. Точка X - произвольная на окружности Эйлера АВС, окружность (XOJ) касается описанной. Все остальные точки и прямые строятся понятно как. Доказать касание.
Да,
🔥4👍2🤡2❤1
Сегодня совместная задача от @BotaynaT2 и @vlad9100
Условие: Дан вписано-описанный четырехугольник, красная точка - центр описанной, синяя - вписанной.
Доказать что центр фиолетовой окружности, центр вписанной и точка пересечения противоположных сторон лежат на одной прямой.
Прикольно
Условие: Дан вписано-описанный четырехугольник, красная точка - центр описанной, синяя - вписанной.
Доказать что центр фиолетовой окружности, центр вписанной и точка пересечения противоположных сторон лежат на одной прямой.
Прикольно
❤15🤡5👍2🔥1🗿1
Такую задачу нам предложил @IvanMChas.
Условие текстом явно понятнее, чем на картинке:
Есть три точки А, В, С. Эллипсы с фокусами в двух из вершин, проходящие через третью, пересекаются попарно в красных, синих и желтых точках. Цветные гиперболы с фокусами в одноцветных точках, проходящие через А, В и С. Они пересекаются в точках А', В', С'. Доказать, что прямые АА', ВВ' и СС' пересекаются в одной точке.
Условие текстом явно понятнее, чем на картинке:
Есть три точки А, В, С. Эллипсы с фокусами в двух из вершин, проходящие через третью, пересекаются попарно в красных, синих и желтых точках. Цветные гиперболы с фокусами в одноцветных точках, проходящие через А, В и С. Они пересекаются в точках А', В', С'. Доказать, что прямые АА', ВВ' и СС' пересекаются в одной точке.
🔥7😍6
А вот и вторая задача в канале от @Edinburgh_of_the_Seven_Seas, условие которой занимает аж две картинки 🤯 .
В треугольнике АВС угол А равен 60°, Be - центр описанной окружности треугольника из эксцентров. Точка P определяется как на первой картинке, а просится доказать равенство пунктирных отрезков на второй картинке...
В треугольнике АВС угол А равен 60°, Be - центр описанной окружности треугольника из эксцентров. Точка P определяется как на первой картинке, а просится доказать равенство пунктирных отрезков на второй картинке...
Please open Telegram to view this post
VIEW IN TELEGRAM
Please open Telegram to view this post
VIEW IN TELEGRAM
Дан треугольник ABC, каждая его сторона не более 2. За ход разрешается отразить какую-то вершину относительно центра масс текущих трех точек. Может ли A удалится на расстояние больше, чем 3 от изначального?
@egfed предложил нам вот такую задачу (скучали по недобрым? 😁 ).
В треугольнике АВС отметили точку Апполония Ap. Четырёхугольники BA_1ApC, BA_2ApC, ... - гармонические. Доказать, что треугольники А_1В_1С_1 и А_2В_2С_2 имеют общую описанную окружность и эллипс Брокара (вписаный эллипс с фокусами в точках Брокара треугольника).
В треугольнике АВС отметили точку Апполония Ap. Четырёхугольники BA_1ApC, BA_2ApC, ... - гармонические. Доказать, что треугольники А_1В_1С_1 и А_2В_2С_2 имеют общую описанную окружность и эллипс Брокара (вписаный эллипс с фокусами в точках Брокара треугольника).
Please open Telegram to view this post
VIEW IN TELEGRAM
🔥12
Вот такая задача от @Savva_Morozkin
H - ортоцентр. То, что кажется прямоугольником - прямоугольник. Дальше вроде условие понятно из картинки
H - ортоцентр. То, что кажется прямоугольником - прямоугольник. Дальше вроде условие понятно из картинки
❤8🔥2👏2
Скучали по задачкам от @Mamonovclhgffkuffhj?))
Вот такая прикольная имеется.
В треугольнике АВС O, I_a, Na, Fe - центры описанной и вневписанной окружностей, точки Нагеля и Фейербаха. Доказать, что прямые AFe и OI_a пересекаются на стороне ВС <=> Na лежит на OI_a.
Вот такая прикольная имеется.
В треугольнике АВС O, I_a, Na, Fe - центры описанной и вневписанной окружностей, точки Нагеля и Фейербаха. Доказать, что прямые AFe и OI_a пересекаются на стороне ВС <=> Na лежит на OI_a.
Forwarded from Ботаем геому (Тихомир Листожуй)
Устная олимпиада по геометрии 2025
Вдохновившись опытом предыдущего года, мы решили сделать устную олимпиаду по геометрии НИУ ВШЭ традиционной!
В этом году олимпиада проводится для учеников 8–11 классов в трёх параллелях: 8, 9 и 10–11 классов.
Чтобы не утруждать вас отборами, сразу на заключительный этап допускаются дипломаты любых перечневых олимпиад по математике.
Если дипломов ещё нет, то несложный отбор всё-таки придётся пройти. Подробности о том, как он проходит, можно найти на сайте. Там же можно найти задания и решения олимпиады прошлого года и другую полезую информацию.
Для участия необходима предварительная регистрация, доступная по ссылке.
(Если планируете участвовать, то зарегаться лучше сейчас, так как сайт вышки имеет свойство уходить на тех. обслуживание в рандомный момент времени)
Вдохновившись опытом предыдущего года, мы решили сделать устную олимпиаду по геометрии НИУ ВШЭ традиционной!
В этом году олимпиада проводится для учеников 8–11 классов в трёх параллелях: 8, 9 и 10–11 классов.
Чтобы не утруждать вас отборами, сразу на заключительный этап допускаются дипломаты любых перечневых олимпиад по математике.
Если дипломов ещё нет, то несложный отбор всё-таки придётся пройти. Подробности о том, как он проходит, можно найти на сайте. Там же можно найти задания и решения олимпиады прошлого года и другую полезую информацию.
Для участия необходима предварительная регистрация, доступная по ссылке.
(Если планируете участвовать, то зарегаться лучше сейчас, так как сайт вышки имеет свойство уходить на тех. обслуживание в рандомный момент времени)
🔥5🥰3👏2
@n_1_8_27_64_125_216_343 поведал такой красивый факт.
ABCD - вписанный четырёхугольник, тогда аж восемь инцентров понятно каких треугольников лежат на одной конике
ABCD - вписанный четырёхугольник, тогда аж восемь инцентров понятно каких треугольников лежат на одной конике
🔥17👍4❤2
На втором туре ЮМТ сегодня предложили ещё одну совсем простенькую задачу от меня, Димы Крохалева и Саши Коваленко.
Условие:
Условие:
Дан треугольник 𝐴𝐵𝐶 с углом ∠𝐴𝐵𝐶 = 45°, его высоты из вершин 𝐴 и 𝐶 пересекают (𝐴𝐵𝐶) в точках 𝐸, 𝐷. Пусть 𝐺 — пересечение касательных к (𝐴𝐵𝐶) в 𝐴, 𝐶. Докажите, что ортоцентр 𝐷𝐸𝐺 лежит на 𝐴𝐶.
🗿6❤4👍4