Моя авторка вот такой красивый факт недавно нашел.

В треугольнике АВС О - центр описанной окружности, Fe - точка Фейербаха. Касательные ко вписанной окружности и (ВОС) пересекаются в точке D. Доказать, что AD, AFe - изогонали

Закинул эту задачу в геометрический марафон:

(Новое применение этого чата)

Оказывается, что три окружности, каждая из которых касается трех вневписанных как на рисунке, имеют общую точку.

@MeZox_111 сообщил такую красоту

Олимпиада НИУ ВШЭ по геометрии

Наконец стала известна дата, так что:

Устная олимпиада по геометрии НИУ ВШЭ пройдет 23 ноября.


В этом году олимпиада проводится для учеников 8–11 классов в трёх параллелях: 8, 9 и 10–11 классов.

Чтобы не утруждать вас отборами, сразу на заключительный этап допускаются дипломанты любых перечневых олимпиад по математике.

Если дипломов ещё нет, то несложный отбор всё-таки придётся пройти. Подробности о том, как он проходит, можно найти на сайте. Там же можно найти задания и решения олимпиады прошлого года и другую полезую информацию.

Для участия необходима предварительная регистрация, доступная по ссылке.

(Если планируете участвовать, то зарегаться лучше сейчас, так как сайт вышки имеет свойство уходить на тех. обслуживание в рандомный момент времени)



P.S. Как жюри хочу сказать, что мы подобрали очень крутые варианты и олимпиада действительно будет насыщена красивыми задачами и новыми конструкциями. Так что всем рекомендую принять участие.

А почему бы не запостить классное геом.неравенство...

В треугольнике АВС AD - биссектриса; оказалось, что вписанные окружности треугольников ABC, ADC касаются. Найти инфинум угла B.

Наконец то задача от подписчика! Сегодня от @kyrovins

В треугольнике АВС Б_a, Б_b, Б_c - соответствующие точки Болтая, АА1, BB1, CC1 - высоты. В треугольниках АB_1C_1, BA_1C_1, CB_1A_1 выбраны понятно какие Болтаи.

a) Доказать подобие черных треугольников на рисунке.

б) Доказать точно такой же факт про точки Шалтая.

Читайте текст, не смотрите на картинку))

@vkomplahposchitaetsa (на самом деле не очень приятно в комплах считается) вот такую задачку нам предложил. Прикольная

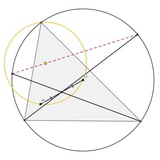
Ib - центр вневписанной окружности треугольника АВС; оказалось что середины синих отрезков лежат на одной пунктирной прямой с А. Доказать, что это высота.

Н - ортоцентр треугольника АВС, М - середина стороны ВС, а P - пересечение MH и (АВС). Доказать, что пунктирная прямая, соединяющая центры красных вписанных окружностей, параллельна ВС.

ABCD - вписанный четырёхугольник, I_a, I_b, I_c, I_d - инцентры треугольников BAD, CBA, DCB, ADC. Красные окружности построены на красных отрезках, как на диаметрах. Доказать, что у них есть радикальный центр.

Классная задача с финала какого-то недавнего Колма.

Ого, нас уже 300
Даже 301

Что-то простенькое.

В треугольнике АВС биссектрисы BE, CD пересекаются в точке I. Доказать, что на прямой Эйлера треугольника BIC есть точка, равноудаленная от B и E, С и D.

Моя задача с устной олимпиады ВШЭ по геометрии, прошедшей сегодня

Точки Х, У - пересечения прямой Эйлера треугольника АВС и сторон АВ, АС. D - пересечение окружности (АВС) и касательной в А к окружности (AOH).
Надо доказать, что онтоцентр треугольника AXY лежит на прямой HD

Поздравляю также наших админов Т.Григорьева и И. Полянского с победой!!

Точка О - центр (красной) равнобокой гиперболы. Точки А, В выбраны на ней так, что угол между касательными в них к гиперболе равен 45°. С - пересечение касательных.

Доказать, что CO^8 (1/CA^4 + 1/CB^4) не зависит от выбора А, В.

Задачка от @don_schijuan.

Докажите внешнюю лемму саваямы

.

Заочный тур Шарыги