ABCD - вписанный четырёхугольник, I_a, I_b, I_c, I_d - инцентры треугольников BAD, CBA, DCB, ADC. Красные окружности построены на красных отрезках, как на диаметрах. Доказать, что у них есть радикальный центр.

Классная задача с финала какого-то недавнего Колма.

Ого, нас уже 300
Даже 301

Что-то простенькое.

В треугольнике АВС биссектрисы BE, CD пересекаются в точке I. Доказать, что на прямой Эйлера треугольника BIC есть точка, равноудаленная от B и E, С и D.

Моя задача с устной олимпиады ВШЭ по геометрии, прошедшей сегодня

Точки Х, У - пересечения прямой Эйлера треугольника АВС и сторон АВ, АС. D - пересечение окружности (АВС) и касательной в А к окружности (AOH).
Надо доказать, что онтоцентр треугольника AXY лежит на прямой HD

Поздравляю также наших админов Т.Григорьева и И. Полянского с победой!!

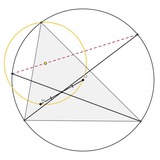
Точка О - центр (красной) равнобокой гиперболы. Точки А, В выбраны на ней так, что угол между касательными в них к гиперболе равен 45°. С - пересечение касательных.

Доказать, что CO^8 (1/CA^4 + 1/CB^4) не зависит от выбора А, В.

Задачка от @don_schijuan.

Докажите внешнюю лемму саваямы

.

Заочный тур Шарыги

В треугольнике АВС А_1, В_1, С_1 - основания высот, синяя окружность - окружность Эйлера (это (A_1B_1C_1)), красная окружность - вписанная, Fe - точка их касания. Вторые касательные в A_1, B_1, C_1 ко вписанной окружности образовали треугольник DEF. Пусть A', B', C' - точки пересечения окружности Эйлера и прямых DFe, EFe, FFe. Доказать, что прямые AA', BB', CC' пересекаются на окружности Эйлера.

Так получилось, что @AlanZar07 нам такое чудо предложил))

Закину авторку.

Дан треугольник АВС, красная точка - его А-Шалтай, фиолетовая - А-Болтай, и оказалось, что прямая через них параллельна ВС. Строится треугольник АВ1С1, такой, что В1 и С1 лежат на ВС и фиолетовая точка - его А-Шалтай. Синяя точка - А-Болтай нового треугольника.

Докажите коллинеарность.

!!! Также напоминаю что если у вас есть геометрическая задача, которая вряд ли попадет на какую то олимпиаду (например, как позапрошлый пост с кучей окружностей), то можете скинуть ее нам - и мы ее запостим :)

Что-то реально красивое в этом канале от @sporegalacticadventures.

AD, BE, CF - высоты АВС, О_9 - центр окружности Эйлера DEF, О - центр описанной окружности, а О_1 - центр окружности (BOC). Доказать равенство углов

У большинства сейчас, наверное, начинается интенсивная подготовка к регу. На реге нынче дают геометрические задачи которые в большинстве своем не считаются и не двигаются в тупую. Поэтому готовьтесь к советщине(термин который обозначает такие задачи)! Вот вам одна такая.

Докажите существование окружности которая касается двух прямых и проходит через 2 точки.

Новогодняя задача от @MigelSa.

D, E, F - точки касания вписанной окружности, голубые, красные и желтые точки - Шалтаи треугольников AED, AFD и аналогичных. Доказать, что три пунктирные окружности проходят через одну точку.

Всех с наступающим 🎄

Здесь уже поздравили, идите решать задачу!