Народная задача!
Автор - величайший @euclid_is_dead.
Условие: Есть вписанный четырёхугольник ABCD и окружность w, касающаяся прямых AB и CD. Через A и B проведена окружность w1, касающаяся w. Через C и D проведена окружность w2, касающаяся w. Пусть l-общая внешняя касательная w1 и w2. Доказать, что существует парабола, проходящая через A, B, C, D и касающаяся l.
Автор - величайший @euclid_is_dead.
Условие: Есть вписанный четырёхугольник ABCD и окружность w, касающаяся прямых AB и CD. Через A и B проведена окружность w1, касающаяся w. Через C и D проведена окружность w2, касающаяся w. Пусть l-общая внешняя касательная w1 и w2. Доказать, что существует парабола, проходящая через A, B, C, D и касающаяся l.
Всех с праздником!
Все админы не дома и не смогут сделать Вам рисунки к задачам, поэтому сегодня без постов)
Upd: ладно, Юсуф дома и м.б. что-то Вам сделает.
Все админы не дома и не смогут сделать Вам рисунки к задачам, поэтому сегодня без постов)
Upd: ладно, Юсуф дома и м.б. что-то Вам сделает.
❤2
Итак, объявляем день разминок на CRL.
Разминка №18.
Пусть точки B, C, D, E, F лежат на одной окружности. Прямые DE и DF пересекают BC в точках X и Y . Пусть описанная окружность треугольника DXY пересекает описанную окружность треугольника BCD в точке Z. Докажите, что E, F, симметрия Z относительно BC и точка T такая, что BDCT - параллелограмм, лежат на одной окружности.
Разминка №18.
Пусть точки B, C, D, E, F лежат на одной окружности. Прямые DE и DF пересекают BC в точках X и Y . Пусть описанная окружность треугольника DXY пересекает описанную окружность треугольника BCD в точке Z. Докажите, что E, F, симметрия Z относительно BC и точка T такая, что BDCT - параллелограмм, лежат на одной окружности.
НАРОДНОЕ CRL ОТ @IvanMChas.
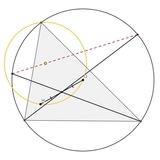
Красная точка - Шалтай красного треугольника, а синяя точка - Шалтай синего треугольника.
Красная точка - Шалтай красного треугольника, а синяя точка - Шалтай синего треугольника.
👎3🤡3❤2🤮2
Опять народное и опять CRL, и опять от @IvanMChas.
Красная точка - Шалтай красного треугольника, синяя - Шалтай синего треугольника, а зеленая точка - центр зеленой окружности на рисунке.
Красная точка - Шалтай красного треугольника, синяя - Шалтай синего треугольника, а зеленая точка - центр зеленой окружности на рисунке.
Всем доброе утро. Нам очень понравилась идея тематических дней, так что сегодня для вас ещё один. День кубик ;) Мы постарались подобрать не классические задачи на кубики, а некоторые более неожиданные факты, так что задачи сегодня будут довольно продвинутые.
Но начнем с довольно простой задачи. Точки P и P' на рисунке изогонально сопряжены.
Но начнем с довольно простой задачи. Точки P и P' на рисунке изогонально сопряжены.
Итак, вторая задача уже сразу довольно интересная. Я думаю, к ней рисунок будет излишним.
Конечная точка такова, что прямая через неё и трилинейный полюс её ортотрансверсали проходит через центроид. Доказать, что эта точка лежит на гиперболе Киперта.
Конечная точка такова, что прямая через неё и трилинейный полюс её ортотрансверсали проходит через центроид. Доказать, что эта точка лежит на гиперболе Киперта.
К четвертой задаче рисунок также будет излишним.
Существует ли остроугольный треугольник, в котором середина отрезка между точками Торричелли лежит вне него?
Существует ли остроугольный треугольник, в котором середина отрезка между точками Торричелли лежит вне него?
Geometry Daily
в канал добавлена новая реакция специально для постов юсуфа
Ненавидь меня это нормально👌😂
Тематический день кубик - ВСЁ. Заказывайте тематические дни в комментариях, м.б. мы сделаем.
👏4