Шокирующие новости! На канале «Geometry Weekly» вышли две задачи за неделю — непорядок.

Точка G — центроид треугольника ABC. Докажите, что точки Лемуана треугольников ABC и A’B’C’ совпадают.

Да, задачу несложно посчитать в векторах/барицентрических. Но интересно подумать и над геометрическими решениями. Самое короткое из известных мне занимает, если немного слукавить, полторы строчки

Задачка попробще. Может, баян

Когда я узнал этот факт несколько лет назад, то сильно удивился. Не существованию, а тому, что не замечал его раньше — настолько классическим он выглядит

P.S. Когда-нибудь я разберусь, как писать сообщения от имени сообщества, и смогу разговаривать с подписчиками

Задача Николая Белухова из журнала KöMaL:

Четырёхугольник ABCD описан вокруг окружности ω. Окружность γ проходит через точки A, C и касается ω в точке P. Общая касательная к ω и γ в точке P пересекает диагональ BD в точке Q. Докажите, что вторая касательная из Q к ω параллельна AC.

Очередной отмыв денег в «ЛУЧШЕМ» техническом университете страны. Спонсирование лудомании под видом благой цели.

— Распоряжение бюджетом. построить 5этажный многоквартирный дом (считайте новую общагу лфишникам) стоит 150кк
платить стобалльникам 100к в 2024 + 200к в 2025 стоит 150кк.

— Инвестиция в таланты. Участник всероса << 100 баллов егэ < призёр всероса << двухстобальнтк ЕГЭ. Да даже так: возьмем человека, который написал профмат на 99 баллов в первую волну и человека, набравшего 80 в основную и 100 на пересдаче в 2025.

— НЕблагая цель. сообщение о выплатах вышло поздно, а значит не было цели популяризировать технические специальности в РФ. К тому же никогда не было избытка свободных мест на физтехе для егэшников. Гораздо лучше было бы провести такую акцию в МГТУ или МИФИ

— Гадость для страны. 100 балльник с баллом 306 переносить документы из бауманки в физтех, надеясь пройти по конкурсу и главное получить 200к. Однако все места на физтехе разобраны бвишниками. И в итоге чел вообще никуда не попал и пролетел даже на первоначальную техническую специальность. Итог: нехватка кадров

— Пропаганда списывания.
Очередной повод списать экзамен. Списать ЕГЭ теперь будут хотеть даже олимпиадники, которым к тому же нечего терять в вопросе поступления.

Таким образом, возможно:
1) на физтехе не умеют распоряжаться бюджетом. Гораздо лучше для страны было бы отправить эти деньги на СВО.
2) Банальный отмыв денег. Уже недавно всплывала новость о коррупции в данном заведении.

Наверное, стоит обратить больше внимание на МИФИ, который к тому же напрямую сотрудничает с Росатомом. Они активно развивают сейчас и IT проекты. А вот буквально несколько часов назад всплыла новость:

В МИФИ подготовят кадры для цифровой экономики РФ, фундаментом проекта станет Wildberries

Я лично сам пойду и перенесу документы с загнивающего Физтеха в расцветающий МИФИ. Советую другим олимпиадникам тоже об этом задуматься, к тому же в мифи их ценят и любят, обзванивают абитуриентов и желают успехов в поступлении, не навязывая выбор.

Я, автор канала PhysicsWeekly уже отправил претензию Мизулиной. Призываю и вас. Распространите.

Думайте.

Physics Weekly. Подписаться

Перевод названия Леммы Рыжик сделал сам. Может у вас получится лучше?

Встречайте новую лемму ARL🔥
Подробно о ней можно будет узнать на научной конференции https://turgor.ru/lktg/

Можно также задать вопросы Юсуфу и Станиславу под этим постом.
Ну а Рыжик пошел отдыхать😻

Этот ролик уже в YouTube https://youtube.com/shorts/4LCis0kBqV4?si=6IGi0LNmemEkdI6J

(Шарыгинская олимпиада 2025, 10.4)

H - ортоцентр серого треугольника
Доказать, что красная прямая проходит через H

Ой простите, я перепутал задачи. Это высшая проба 2026 11.6.

(Задача с aops…🥀🥀🥀)

M - середина BC, A’ - симметрия A относительно DE
Доказать, что DE, IO и A’M пересекаются в одной точке

Какие же вы слабые... Никто даже НЕ ПОПЫТАЛСЯ решить... И. Ф. Шарыгин как-то сказал, что геометрия - это искусство решать ВЕРНУЮ задачу на НЕВЕРНОМ чертеже. Как будто впервые видите рисунок, где прямые, которые должны пересекаться в одной точке, не пересекаются. Это многое говорит о вас...

(Карпов - Каспаров, 1984 [секретная партия])

Дан треугольник c3e5g3. Черные пешки — эксцентры, слоны — точки касания вписанной окружности со стороной. Ладья — инцентр, конь центр описанной. Докажите, что прямые пешка — слон (соответственные) пересекаются на прямой ладья — конь.

С Саввой Чуевым (не геи)

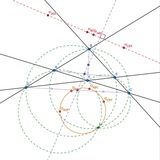
Поляры точки Бевена треугольника ABC относительно вневписанных окружностей треугольника ABC образовали треугольник XYZ. Пусть PQR - половинный треугольник, Be' - изогональное сопряжение точки бевена PQR в треугольнике PQR. T - проекция Be' на QR. Докажите, что AX,BY,CZ, PT пересекаются в одной точке.

Задача №4*

В треугольнике ABC выбраны точки PQR на сторонах BC, AC, AB. Так, что BP/PC=CQ/QA=AR/RB=1/2. Найдите площадь треугольника образованного прямыми AP, BQ, CR если площадь ABC 10416.

Чат для обсуждения геометрии


Около 4 месяцев назад был закрыт чат канала Олимпиадная Геометрия, ставший большим централизованным местом для обсуждения геометрии. После закрытия того чата была предпринята попытка полного отказа от цензуры, которая не увенчалась успехом по понятным причинам, поэтому:

Мы — Юсуф Нагуманов, Дима Герасимов и Петя Ким представляем Вам новый чат для обсуждения геометрии.
Идея заключается в создании крупного модерируемого чата, в котором будет исключительно здравое обсуждение геометрии разного уровня.

Заходите, всем будем рады:
https://news.1rj.ru/str/olympgeomchat

Устная олимпиада по геометрии НИУ ВШЭ 2025 10-11.6