Народная задача от @Edinburgh_of_the_Seven_Seas.

Красиво ⭐️
(Точка А сверху)

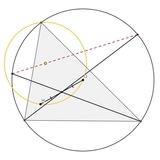
Загадочная народная задача от @mamonovclhgffkuffhj.

Доказать, что существует вписанный в треугольник эллипс, проходящий через его точки Жергонна и Нагеля, с центром в точке Фейербаха его серединного треугольника.

Upd: наблюдения от @don_schijuan: на этом эллипсе также лежат внутренняя точка Маннгейма (изогонально сопряженная Na) и Х_12. А также NaGe - это поляра центроида

Красивая, но пугающая авторка @don_schijuan.

Точки Х, У, Z на картинке - пересечения эллипса Мандара и вписанной окружности треугольника АВС, отличные от его точки Фейербаха. Доказать, что прямые AX, BY, CZ пересекаются в точке, изогонально сопряженной точке Жергонна.

У нас накопилось много ваших задач, мы постараемся опубликовать все в течение двух недель...

Чтобы разбавить задачи в канале, предлагаем порешать эту задачу в качестве утренней разминки.

Дан треугольник ABC с центром описанной окружности O. Точку D выбрали на прямой AO. Пусть E, F - отражения D относительно сторон AC, AB, а E' и F' - изогонально сопряжённые точки к точкам E и F (в ABC). Докажите, что прямые DX, Е'F' перпендикулярны, где X - пересечение прямых BE, CF.

Красивая народная задача от @wargkul.

Доказать, что точка O на рисунке попадает на прямую FE тогда и только тогда, когда прямые BX, CY, AM пересекаются в одной точке.

Красивая и добрая задача от @MeZox_111.

На рисунке O, I, Ia - центры описанной, вписанной и вневписанной окружностей; N - середина большой дуги, а I' - отражение I относительно О.
Доказать, что DI' = IaI'.

Сегодня снова задача от @MeZox_111, но посложнее.

На рисунке Х, У - центры окружностей, G - отражение А относительно ED, а Н - ортоцентр треугольника.

Довольно красивая, но очень недобрая задача от @mamonovclhgffkuffhj.

На картинке I, O, H, G, Na, Fe - центры вписанной и описанной окружностей, ортоцентр, точки Жергонна, Нагеля и Фейербаха какого-то треугольника, а Ш - Fe-точка Шалтая треугольника HFeNa.

Забавный факт от @paleev4.

Синие и красные отрезки равны между собой. Х314 - точка, изотомически сопряжённая ортоцентру треугольника из точек касания вписанной окружности со сторонами.

Прикольная задача от @Mamonovclhgffkuffhj.

На рисунке О и Н - центр описанной окружности и ортоцентр АВС, Х110 - фокус параболы Киперта (т.е. такая точка на описанной окружности, отражения которой относительно АВ, АС, ВС попадают на ОН), L - точка де Лоншана (т.е. отражение Н относительно О), а L' - изогонально сопряженная точка к ней. Доказать перпендикулярность пунктирных прямых.

Завтра будет продолжение этой конструкции...

Итак, продолжение вчерашнего поста от @timofeyxd.

D, E, F - середины сторон треугольника АВС.

а) Доказать касание с окружностью Эйлера на рисунке.

б) Доказать, что радикальный центр трех окружностей, определенных аналогично пунктирной на рисунке для вершин А, В, С; лежит на прямой Эйлера.

Следующие несколько постов будут тоже относиться к одному сюжету...

Задача от @IvanMChas, снова на Шалтайную тематику.

а) Доказать, что три прямые на рисунке пересекаются в одной точке, где Ш(...) - L-Шалтаи соответствующих треугольников, а L - точка Лемуана.

б) Найти ГМТ таких точек L, для которых верно условие.
Подсказка: оно также проходит через точки Торричеллии, Апполония, центроид и почему-то точку Фейербаха.