Вчера был выходной 😁

Upd: оба админа, которые делают рисуночки, заболели, поэтому объявляется неделя стереомы, кг и неравенств

Интернет не анонимен

Кто-то пожаловался в комментариях, что предыдущая разминка была слишком простой.
Итак, РАЗМИНКА 24.

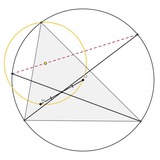
В треугольнике АВС угол В тупой, а H и I - его ортоцентр и инцентр. Доказать, что HI не больше, чем 4S(AHC)/P(ABC).

Ну и в завершение дня предлагаем вам решить очень красивую народную задачу от @IvanMChas.

Бс, Бb - C-Болтай AFC и B-Болтай АFB.

Доброе утро! Разминка №25.

Дан выпуклый многоугольник, никакие две стороны которого не параллельны. Для каждой из его сторон рассмотрим угол, под которым она видна из вершины, наиболее удалённой от этой стороны. Доказать, что сумма всех таких углов равна 180°.

Разминка №26

Наверное моё любимое нер-во...

Внутри окружности радиуса R расположено n точек. Докажите, что сумма квадратов попарных расстояний между ними не превосходит (nR)^2.

Вместо 27-ой разминки предлагаем вам решить добрейшую авторку @Edinburgh_of_the_Seven_Seas.

В треугольнике АВС DEF - чевианный треугольник точки G. Оказалось, что пересечения окружностей (DEG), (DFG), (EFG) со сторонами треугольника лежат на одной окружности. Построить все такие точки G.

Разминка 28.

Дан тетраэдр ABCD. Плоскость a пересекает AB, BC, CD, DA в точках X,Y,Z,T. Оказалось, что XYZT лежат на одной окружности с диаметром XZ. Пусть P - точка пересечения касательных к этой окружности в Y и T. Докажите, что P лежит в одной плоскости с серединами AB, BC, CD, DA.

Народная задача от @IvanMChas

Доказать параллельность трех прямых на рисунке (из Шалтаев, Болтай туда случайно затесался) при том что:
Б_A - А - болтай в АВС, Ш_AB - Б_A - шалтай в AБ_AB и тд.

Разминка 29.

Самая смешная задача в мире.

Народный шедевр от @sqrt_MCh

Дан треугольник АВС и точка P внутри него. Пусть Xa - точка микеля четырёхсторонника {АВ, АС, BP, CP}. Точки Xb и Xc определим аналогично.

Доказать, что:
а) треугольники АВС и XaXbXc перспективны.

б) В треугольнике XaXbXc точки P и Q изогонально сопряжены.

Админы устали делать разминки, т.к это однообразно и засоряет канал. Мы хотим отказаться от разминок и сделать новую рубрику. В связи с тем, что этот канал НАРОДНЫЙ :), мы предлагаем вам писать идеи для этой рубрики в комментарии. Самую интересную и креативную мы воплотим в жизнь. :)

Народная задача от @don_schijuan.

Красная точка на рисунке - фокус вписанной параболы.

теперь в канале будет по 2-3 поста в неделю, т.к. тогда он не засоряется и становиться более читабельным и приятным

Народная задача от @Edinburgh_of_the_Seven_Seas.

Красиво ⭐️
(Точка А сверху)

Загадочная народная задача от @mamonovclhgffkuffhj.

Доказать, что существует вписанный в треугольник эллипс, проходящий через его точки Жергонна и Нагеля, с центром в точке Фейербаха его серединного треугольника.

Upd: наблюдения от @don_schijuan: на этом эллипсе также лежат внутренняя точка Маннгейма (изогонально сопряженная Na) и Х_12. А также NaGe - это поляра центроида

Красивая, но пугающая авторка @don_schijuan.

Точки Х, У, Z на картинке - пересечения эллипса Мандара и вписанной окружности треугольника АВС, отличные от его точки Фейербаха. Доказать, что прямые AX, BY, CZ пересекаются в точке, изогонально сопряженной точке Жергонна.

У нас накопилось много ваших задач, мы постараемся опубликовать все в течение двух недель...

Чтобы разбавить задачи в канале, предлагаем порешать эту задачу в качестве утренней разминки.

Дан треугольник ABC с центром описанной окружности O. Точку D выбрали на прямой AO. Пусть E, F - отражения D относительно сторон AC, AB, а E' и F' - изогонально сопряжённые точки к точкам E и F (в ABC). Докажите, что прямые DX, Е'F' перпендикулярны, где X - пересечение прямых BE, CF.

Красивая народная задача от @wargkul.

Доказать, что точка O на рисунке попадает на прямую FE тогда и только тогда, когда прямые BX, CY, AM пересекаются в одной точке.

Красивая и добрая задача от @MeZox_111.

На рисунке O, I, Ia - центры описанной, вписанной и вневписанной окружностей; N - середина большой дуги, а I' - отражение I относительно О.
Доказать, что DI' = IaI'.

Сегодня снова задача от @MeZox_111, но посложнее.

На рисунке Х, У - центры окружностей, G - отражение А относительно ED, а Н - ортоцентр треугольника.