Задача 34:
Автор - GeoGen, Ким Пётр

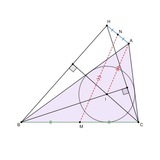
В треугольнике ABC I - инцентр, L - середина дуги (BAC). Точка S на окружности (ABC) такова, что угол ASI - прямой. LS пересекает CI в точке X. D - точка касания вписанной окружности ABC со стороной AC. K - середина дуги (BC) окружности (ABC), не содержащей A.
Доказать, что угол XDK - прямой.

Задача 35:
Автор - GeoGen, Ким Пётр

В треугольнике ABC I - инцентр, а M - середина стороны BC. A1 - отражение A относительно прямой IM. A2 - отражение A1 относительно AB.
Доказать, что окружность (AA1A2) касается перпендикуляра из I на BC.

Задача 36:
Автор - GeoGen, Пучков Пётр

Четырëугольник ABSC - гармонический. M - середина его диагонали BC, а D - произвольная точка на второй диагонали AS. Прямая DM пересекает AB и AC в точках P и Q.
Доказать, что окружность (APQ) касается окружности (SMD)

Задача 37:
Автор - GeoGen, Ким Пётр

В треугольнике ABC I - центр вписанной окружности. Точка S на окружности (ABC) такова, что угол ASI - прямой. D - точка касания вписанной окружности со стороной BC. M - середина дуги BAC окружности (ABC)
Доказать, что окружность с центром в M, проходящая через A касается (BDS) и (CDS).

Задача 38:
Автор - GeoGen, Пучков Пётр

В треугольнике ABC I - центр вписанной окружности, а X и Y - точки касания вписанной окружности со сторонами AC и AB. N - середина дуги BAC, а Z - точка пересечения (CXN) и (BYN), отличная от N.
Доказать, что угол ZMI прямой, где M - середина BC

Задача 39:
Автор - GeoGen, Ким Пётр

В треугольнике ABC N - середина дуги (BAC). I - его инцентр, а M - середина стороны BC. J - инцентр треугольника BIN. Прямые IJ и MN пересекаются в точке K.
Доказать, что окружность (BNJ) касается (KIM).

Задача 40:
Автор - Ким Пётр, GeoGen

В треугольнике ABC w - вписанная окружность, а I - её центр. w касается BC в точке D. На отрезках BI и CI взяты точки E и F такие, что IE = IF. M - середина отрезка EF. Окружность (IMD) вторично пересекает w в точке P. Прямая AP вторично пересекает (IMD) в точке Q.
Доказать, что I, E, F, Q лежат на одной окружности.

Уважаемые подписчики!
В ближайшее время (скорее всего завтра) мы планируем разобрать некоторые задачи из канала в формате стрима.
Какие задачи Вы бы хотели увидеть на разборе?

Уважаемые подписчики!
Стрим с разбором задач состоится завтра (31 декабря) в 12:00 (дня) по мск
Предварительный список задач: 16, 24, 25, 26, 28, 32, 36, 38, 39, 40

Можно присоединяться к конференции, планируем начать через 10 минут
https://jazz.sber.ru/ebsf5i?psw=OAoAEhgCEk4PGgcERxYFXQAQGg

Начинаем разбор. Порядок разбора задач следующий:
16, 36, 28, 24, 40, 25, 38, 26, 39, 32

Задача 41:
Автор - Ким Пётр

В треугольнике ABC точки X1, Y1 выбраны на стороне AB, X2, Y2 на стороне AC, а X3, Y3 на стороне BC таким образом, что X1Y2 параллелен X2Y1 параллелен BC, X3Y1 параллелен Y3X1 параллелен AC, X2Y3 параллелен Y2X3 параллелен AB.
Доказать, что середина отрезка между центрами (X1X2X3) и (Y1Y2Y3) лежит на прямой Эйлера треугольника ABC.

Задача 42:
Автор - GeoGen, Пучков Пётр, Чуев Савва

#37 (Высшая проба 2024, 10.3)

В треугольнике ABC точка I — центр вписанной окружности, E и F — основания биссектрис BI и CI соответственно. Прямая AI пересекает описанную около треугольника EIF окруж- ность в точке T != I. H - ортоцентр треугольника AEF. Доказать, что ортоцентр треугольника AEF равноудален от точек T и I

Задача 43:
Автор - GeoGen, Пучков Пётр

В треугольнике ABC I - центр вписанной окружности, N - точка Нагеля, F - точка Фейербаха, H - ортоцентр. X - симметрична I относительно F. Докажите, что окружность (IHX) касается прямой HN

Задача 44:
Автор - Чуев Савва

H - ортоцентр треугольника ABC. Окружность с центром в середине BC, проходящая через H, пересекает BC в точках A1 и A2. Аналогично определяются точки B1, B2, C1, C2. Докажите, что ортоцентры треугольников ABC, A1B1C1 и A2B2C2 лежат на одной прямой.

Задача 45:
Автор - GeoGen, Ким Пётр

В треугольнике ABC I - центр вписанной окружности, а D - её точка касания со стороной  BC. Отражение D относительно середины BC - точка E. A' - диаметрально противоположная точке A на окружности (ABC). G - проекция D на прямую через A' параллельную BC.
Докажите, что (DEG) касается (ABC).