В 1796 году, когда великому математику Гауссу было 18 лет, он обнаружил, что правильный 17-угольник можно построить, используя только линейку и циркуль.
Сати в своем Facebook опубликовал тайскую версию с замечанием
Неоднозначное コンパス (компас) было переведено как เข็มทิศ (навигационный компас), который отличается от วงเวียน (инструмента для рисования окружностей).
1🔥7👍2😱2❤🔥1
Forwarded from Makar Lopatin
Задача №11
Можем ли мы на самом деле построить правильный 17-угольник, используя линейку без делений и навигационный компас?
То есть компас — это идеальная окружность с неизвестными центром и радиусом, с иглой, которая всегда указывает на север. Вы можете разместить компас так, чтобы его край проходил через 0, 1 или 2 точки, обвести его край и отметить точку на окружности, в которую указывает игла.
Манга
Можем ли мы на самом деле построить правильный 17-угольник, используя линейку без делений и навигационный компас?
То есть компас — это идеальная окружность с неизвестными центром и радиусом, с иглой, которая всегда указывает на север. Вы можете разместить компас так, чтобы его край проходил через 0, 1 или 2 точки, обвести его край и отметить точку на окружности, в которую указывает игла.
Манга
1👍7🔥3👌2❤1
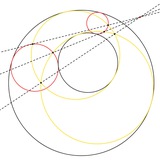
Задача №24
Оранжевые окружности -- окружность проходящая через A, касающаяся BC и (ABC), аналогично определяются две другие окружности (w_A,w_B,w_C)
Красные окружности -- окружность касающаяся BC и касательные в точках B и C к (ABC),аналогично определяются две другие окружности (Г_A,Г_B,Г_C)
Докажите что существует окружность касающаяся 8 следующих окружностей: w_A,w_B,w_C,Г_А,Г_В,Г_С,впис.,окружность Моисея(Moses Circle)
❤🔥9🤯4🔥3❤2👍1
Разминка №12 #авторская
AA_1,BB_1,CC_1 пересекаются в точке X. (CA_1B_1),(BA_1C_1),(AB_1C_1) пересекаются в M. (ABB_1),(ACC_1) пересекаются в A_2 (аналогично определяются B_2,C_2). Докажите что (AB_2C_2),(BA_2C_2),(CA_2B_2) пересекаются в точке P, (B_1A_1C_2),(C_1A_1B_2),(C_1B_1A_2) пересекаются в точке L.
Окружности (LC_2C_1),(LA_2A_1),(LB_2B_1),(C_2XC),(A_2XA),(B_2XB),(BA_2C),(CB_2A),(AC_2B) пересекаются в точке J
J,P,M лежат на одной прямой
AA_1,BB_1,CC_1 пересекаются в точке X. (CA_1B_1),(BA_1C_1),(AB_1C_1) пересекаются в M. (ABB_1),(ACC_1) пересекаются в A_2 (аналогично определяются B_2,C_2). Докажите что (AB_2C_2),(BA_2C_2),(CA_2B_2) пересекаются в точке P, (B_1A_1C_2),(C_1A_1B_2),(C_1B_1A_2) пересекаются в точке L.
Окружности (LC_2C_1),(LA_2A_1),(LB_2B_1),(C_2XC),(A_2XA),(B_2XB),(BA_2C),(CB_2A),(AC_2B) пересекаются в точке J
J,P,M лежат на одной прямой
👍8🔥6❤🔥4💊1