На той же олимпиаде ЮМШ в 9 классе был предложен такой геометрический сюжет.
Дан неравнобедренный треугольник ABC без тупых углов, с центром вписанной окружности I и точкой
M, делящей отрезок BC пополам.
1.1. Докажите, что прямая IM не может быть параллельна никакой стороне треугольника ABC.
1.2. Пусть прямая IM пересекает прямые AB и AC в точках C1 и B1, соответственно. Обозначим
через I_b центр вневписанной окружности треугольника ABC, касающейся отрезка AC. Докажите, что
I_bB1 параллельно BC. (Т. Праведников, Н. Галимуллин)
Вывод.
1.3. Пусть ∠A = 90. Точка P выбрана так, что MP = MI и IP параллельно BC. Докажите, что IP ⩽ B1C1.
1.4. Обозначим через N середину дуги BAC описанной окружности треугольника ABC. Докажите,
что центр описанной окружности треугольника NB1C1 лежит на прямой AI. (Т. Праведников, Н. Галимуллин)
Дан неравнобедренный треугольник ABC без тупых углов, с центром вписанной окружности I и точкой
M, делящей отрезок BC пополам.
1.1. Докажите, что прямая IM не может быть параллельна никакой стороне треугольника ABC.
1.2. Пусть прямая IM пересекает прямые AB и AC в точках C1 и B1, соответственно. Обозначим
через I_b центр вневписанной окружности треугольника ABC, касающейся отрезка AC. Докажите, что
I_bB1 параллельно BC. (Т. Праведников, Н. Галимуллин)
Вывод.
1.3. Пусть ∠A = 90. Точка P выбрана так, что MP = MI и IP параллельно BC. Докажите, что IP ⩽ B1C1.
1.4. Обозначим через N середину дуги BAC описанной окружности треугольника ABC. Докажите,
что центр описанной окружности треугольника NB1C1 лежит на прямой AI. (Т. Праведников, Н. Галимуллин)
👍11❤2
Геометрия-канал
На той же олимпиаде ЮМШ в 9 классе был предложен такой геометрический сюжет. Дан неравнобедренный треугольник ABC без тупых углов, с центром вписанной окружности I и точкой M, делящей отрезок BC пополам. 1.1. Докажите, что прямая IM не может быть параллельна…
В 10 классе был такой геометрический сюжет.
Дан остроугольный неравнобедренный треугольник ABC и на его биссектрисах BE и CF, которые
пересекаются в точке I, выбрали такие точки B_1 и C_1, соответственно, что ∠BAB_1 = ∠CAC_1 = 90.
1.1. Оказалось, что ∠A = 60. Докажите, что прямая, соединяющая центры описанных окружностей
треугольников ABC_1 и ACB_1, проходит через I.
1.2. Докажите, что B_1C_1 ⩾ AB + AC − BC.
Вывод
1.3. Описанные окружности треугольников AB_1F и AC_1E повторно пересекаются в точке S. Докажите,
что описанная окружность треугольника AIS проходит через основание перпендикуляра из I на BC.
1.4. Точка X выбрана на отрезке B_1C_1 так, что AX ⊥ BC. Докажите, что вневписанные окружности
треугольников AXB_1 и AXC_1, касающиеся отрезка AX, имеют равные радиусы.
Дан остроугольный неравнобедренный треугольник ABC и на его биссектрисах BE и CF, которые
пересекаются в точке I, выбрали такие точки B_1 и C_1, соответственно, что ∠BAB_1 = ∠CAC_1 = 90.
1.1. Оказалось, что ∠A = 60. Докажите, что прямая, соединяющая центры описанных окружностей
треугольников ABC_1 и ACB_1, проходит через I.
1.2. Докажите, что B_1C_1 ⩾ AB + AC − BC.
Вывод
1.3. Описанные окружности треугольников AB_1F и AC_1E повторно пересекаются в точке S. Докажите,
что описанная окружность треугольника AIS проходит через основание перпендикуляра из I на BC.
1.4. Точка X выбрана на отрезке B_1C_1 так, что AX ⊥ BC. Докажите, что вневписанные окружности
треугольников AXB_1 и AXC_1, касающиеся отрезка AX, имеют равные радиусы.
❤11
Forwarded from Геометрия с Ниловым
Докажите, что точка Содди S лежит на одной прямой с инцентром I и точкой Жергона G.
❤8🥰3😁2
Forwarded from Митя и Дима
На этой неделе у замечательного Учителя, Григория Борисовича Филипповского, был День Рождения! ☀️
Отличный повод рассказать, что сайт Григория Борисовича обновился — там теперь доступны новые статьи автора!
Приятного (геометрического) чтения! ☕️
Отличный повод рассказать, что сайт Григория Борисовича обновился — там теперь доступны новые статьи автора!
Приятного (геометрического) чтения! ☕️
👍23❤11👎2😁1
Forwarded from Геометрия с Ниловым
Задача И.Ф. Шарыгина.
В треугольнике провели три чевианы. Оказалось, что два четырехугольника, образованные парой чевиан и сторонами, к которым они проведены, являются описанными. Докажите, что и третий четырехугольник также описанный.
В треугольнике провели три чевианы. Оказалось, что два четырехугольника, образованные парой чевиан и сторонами, к которым они проведены, являются описанными. Докажите, что и третий четырехугольник также описанный.
❤13
Forwarded from Геометрия с Ниловым
На картинке 4 узла клетчатой бумаги лежат на одной окружности, координаты центра которой не являются целыми или полуцелыми. Могут ли 5 (или больше) узлов клетчатой бумаги лежать на одной окружности, координаты центра которой не являются целыми или полуцелыми?
❤13🤷♂1
Forwarded from Геометрия с Ниловым
This media is not supported in your browser
VIEW IN TELEGRAM
Через три фиксированные точки проводятся прямые, образующие правильный треугольник. Тогда центры всех таких треугольников лежат на одной окружности.
❤30🥰3👍2
Петр Ким, Алексей Суворов — Геометрия окружностей
https://us02web.zoom.us/j/88984633491?pwd=9tuB7ApHDBFatWCgzSaYIDkydwWFeh.1
Математический кружок, вторник 30 декабря
15:30 — 17:00 GMT+3
В докладе будет рассказано про модели евклидовой и неевклидовой геометрии окружностей в параболической геометрии и использование последней для доказательства различных теорем. Будет упомянут аналог этой конструкции над произвольным полем.
Также будет рассказано про попытки придумать аксиоматику геометрии окружностей.
https://us02web.zoom.us/j/88984633491?pwd=9tuB7ApHDBFatWCgzSaYIDkydwWFeh.1
Математический кружок, вторник 30 декабря
15:30 — 17:00 GMT+3
В докладе будет рассказано про модели евклидовой и неевклидовой геометрии окружностей в параболической геометрии и использование последней для доказательства различных теорем. Будет упомянут аналог этой конструкции над произвольным полем.
Также будет рассказано про попытки придумать аксиоматику геометрии окружностей.
😍13👍6
Forwarded from Геометрия с Ниловым
Найдите отношение площади произвольного (зеленого) четырехугольника к площади (красного) треугольника с вершинами в точке пересечения противоположных сторон и серединах диагоналей. Выведите отсюда теорему Гаусса о том, что середины диагоналей и середина отрезка, соединяющего точки пересечения противоположных сторон, лежат на одной прямой.
❤14🤔3
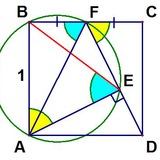
ABCD квадрат. Угол, обозначенный как прямой, прямой.
Доказать, что сумма радиусов серых кругов равна сумме радиусов белых кругов.
// Задачу взял из новой подборки коллег Мухина и Швецова https://news.1rj.ru/str/d_m_podkast/31
Доказать, что сумма радиусов серых кругов равна сумме радиусов белых кругов.
// Задачу взял из новой подборки коллег Мухина и Швецова https://news.1rj.ru/str/d_m_podkast/31
🤔6❤3👍3🔥2
9 и 10 января Профиматика проводит геометрическую онлайн-конференцию для учителей.
Регистрация: https://prfmtk.ru/xVgQBb
Регистрация: https://prfmtk.ru/xVgQBb
👍11👎3
Forwarded from Непрерывное математическое образование
https://www.mathedu.ru/text/shnol_i_dr_sistema_otkrytyh_zadach_po_geometrii_7_klass_2009/
https://www.mathedu.ru/text/shnol_i_dr_sistema_otkrytyh_zadach_po_geometrii_8_klass_2009/
в @school_maths_ru напомнили такие брошюры (Д.Э.Шноль, А.И.Сгибнев, Н.М.Нетрусова)
хочется тж привести фрагмент предисловия:
https://www.mathedu.ru/text/shnol_i_dr_sistema_otkrytyh_zadach_po_geometrii_8_klass_2009/
в @school_maths_ru напомнили такие брошюры (Д.Э.Шноль, А.И.Сгибнев, Н.М.Нетрусова)
хочется тж привести фрагмент предисловия:
В течение нескольких лет в школе «Интеллектуал» использовались листки при изучении геометрии в сильных математических группах (…). За это время применение листков в «Интеллектуале» заметно эволюционировало.
Во-первых, задачи в наших листках по возможности формулируются открыто (…).
Во-вторых, мы заметили, что ученики, работая самостоятельно, часто изобретают длинные, корявые, «технические» решения вместо коротких, красивых и «идейных», которые им мог бы рассказать учитель. Другое дело, что красоту этих решений без самостоятельного поиска трудно оценить. Чтобы сбалансировать эти поиски и работу учеников под руководством педагога, мы ввели следующие «правила игры» :
— учитель помогает на этапе решения (причем играет роль не столько инструктора, сколько научного руководителя: обсуждает, на какой стадии решения находится ученик, куда можно двигаться дальше и т.д.);
— к сложным задачам прилагаются подсказки; ученик сам решает, читать ли их и когда читать;
— раз в три-четыре урока проводятся семинары, на которых учитель обсуждает (…) основные понятия, трудные теоремы, разные решения задач, взаимосвязи между задачами, ставит новые задачи. (…)
В-третьих, мы увидели, что, работая только по листкам, ученики (…) недостаточно хорошо овладевают навыками. (…) Чтобы справиться с этим, мы ввели:
— домашние задания по обычному учебнику и задачнику с классическими задачами;
— математические диктанты, состоящие из нескольких простых задач. Они проводятся почти на каждом уроке в его начале и занимают 5-7 минут. (…)
Следует отметить, что ученики, как правило, общаются друг с другом: (…). Ученик имеет право получить помощь от учителя, одноклассников, учебника. Каждый ученик сам определяет степень самостоятельности своей деятельности.
После изучения темы (листка) проводятся:
— контрольная работа (…);
— устный зачет по теории, на который приглашаются преподаватели других классов (4-5 человек).
(…)
Подчеркнем, что индивидуальная работа не является для нас самоцелью (…). Так, идейно новый материал требует общего вводного разговора (аксиома о параллельных прямых, признаки и свойства параллелограмма, признаки подобия). Важные теоремы требуют эмоционального ударения и их лучше изучать всем вместе (теорема Пифагора, теорема о медианах). Овладеть «техническими» теоремами лучше всего помогают регулярные математические диктанты (теорема Фалеса, вычисление площадей). Красивые решения сложных задач рассказывает учитель (задача Архимеда, прямая Симсона). И т.д. Поэтому приводимые ниже листки следует рассматривать как по необходимости неполную запись «действа», которое ставит учитель вместе с классом.
Библиотека Mathedu.Ru
Шноль Д. Э. и др. Система открытых задач по геометрии, 7 класс. — 2009 // Библиотека Mathedu.Ru
Шноль Д. Э. и др. Система открытых задач по геометрии, 7 класс / Д. Шноль, А. Сгибнев, Н. Нетрусова. — М. : Чистые пруды, 2009. — 32 с. — (Библиотечка «Первого сентября», серия «Математика» ; вып. 28).
❤6