№2 (УстГор 2011, 10-11.3)

Окружность, проходящая через две вершины
а) Трапеции
б) Четырехугольника
пересекает повторно диагонали в зеленых точках, а стороны повторно в фиолетовых точках. Доказать, что оранжевая, зеленая и фиолетовая прямая перекаются в одной точке

№3 (База)

Зеленые прямые - касательные к описанной окружности синего треугольника.
Доказать, что красные точки лежат на одной прямой

№4 (Теорема Паппа)

Условие на картинке
Доказать, что красные точки лежат на одной прямой

#5 (Классика)

Звезда Давида вписана в конику
Доказать, что пунктирные прямые пересекаются в одной точке

№6 (Лемма)

Красная гипербола - образ оранжевой прямой при изотомическом сопряжении относительно данного треугольника. Известно, что оранжевая прямая проходит через центроид.
Доказать, что красная гипербола касается оранжевой прямой

№7 (Классика)

Условие на картинке
Доказать, что красные точки лежан на одной конике

№8 (Баян)

Условие на картинке
Доказать, что фиолетовый треугольник подобен остальным

№9 (Окружность Ламуна)

Красные точки - центры зеленых окружностей
Доказать, что крастные точки лежат на одной окружности

№10 (Классика)

Все углы между серыми прямыми равны. Из синей точки опускаются синие перпендикуляры на серые прямые.
Доказать, что основания этих синих перпендикуляров образуют правильный многоугольник (красный)

№11 (Фольклор)

Условие на картинке
Доказать, что красные прямые параллельны

№12 (Усиление №11)

Условие на картинке
Доказать, что красные прямые перпендикулярны фиолетовой прямой

№13 (Классика)

Зеленые точки - середины соответствующих дуг
Доказать, что красные отрезки равны

№14 (По мотивам древнего региона)

Точки Sh' и Sh - точки Шиффлера треугольников ADK и BCD соответственно
Доказать, что красные точки лежат на одной окружности

№15 (ВсОШ РЭ 2010, 10.3)

Условие на картинке
Доказать, что MANKI - вписанный

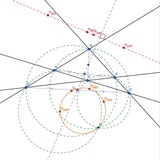
№17 (Полный четырехсторонник)

Дана четверка прямых общего положения

Доказать, что:
а) Окружности (BDE), (ABC), (ADF) и (CEF) пересекаются в одной точке (точка Микеля)

b) Центры окружностей (BDE), (ABC), (ADF) и (CEF) лежат на одной окружности с точкой микеля

c) Середины диагоналей полного четырезсторонника лежат на одной прямой (прямая Гаусса)

d) Ортоцентры треугольников (BDE), (ABC), (ADF) и (CEF) лежат на одной прямой (прямая Обера)

e) Прямая Гаусса перпендикулярна прямой Обера (теорема Гаусса-Боденмиллера)

https://www.geogebra.org/m/zg4wtmrj

Если вы знаете еще замечательные факты про полный четырехсторонник, будет очень здорово, если вы ими поделитесь @geomweeklyauthor

№18 (Argentinian National Olympiad 1995 level 3)

Внутри параллелограмма ABCD взяли такую точку P, что ∠PDA вдвое меньше ∠ABP и ∠PAD вдвое меньше ∠DCP
Доказать, что AB = BP = CP = CD

№19 (Белорусская математическая олимпиада 2019, 9.6)

Синяя окружность касается медианы треугольника
Доказать, что красная пунктирная окружность касается стороны треугольника

№20 (Вспоминаем точку Фейербаха)

Дан треугольник ABC
O - центр описанной окружности
I - центр вписанной окружности
A_0, B_0, C_0 - точки касания вписанной окружности со сторонами.
A_1, B_1, C_1 - основания биссектрис.
M_A, M_B, M_C - середины сторон.
P - точка на прямой OI, P_A, P_B, P_C - основания перпендикуляров из P на стороны треугольника.
K_B - точка пересечения M_A M_C и A_0 C_0. Аналогично определяются K_A и K_B.
M_AI, M_BI, M_CI - середины AI, BI, CI соответственно

Доказать, что:
a) (M_A M_B M_C) касается (A_0 B_0 C_0) (точка Фейербаха)

b) Точка Фейербаха лежит на прямой B_0 K_B

c) Точка Фейербаха лежит на окружности (A_1, B_1, C_1) (теорема Емельяновых)

d) Точка Фейербаха лежит на окружности (P_A, P_B, P_C) (теорема Фонтене)

e) Точка Фейербаха лежит на окружности (B_0, M_AI, M_CI)

f) Попробуйте сформулировать аналогичные утверждения, но для вневписанной окружности

https://geogebra.org/m/n2ejddyd

№21 (Сборник «Математическое просвещение», третья серия, выпуск 7, 2003)

Доказать, что пунктирные окружности касаются

№22 (Теорема Харта)

Доказать, что существует окружность, касающаяся четырех серых окружностей