№15 (ВсОШ РЭ 2010, 10.3)

Условие на картинке
Доказать, что MANKI - вписанный

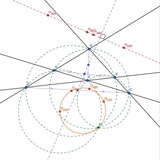
№17 (Полный четырехсторонник)

Дана четверка прямых общего положения

Доказать, что:
а) Окружности (BDE), (ABC), (ADF) и (CEF) пересекаются в одной точке (точка Микеля)

b) Центры окружностей (BDE), (ABC), (ADF) и (CEF) лежат на одной окружности с точкой микеля

c) Середины диагоналей полного четырезсторонника лежат на одной прямой (прямая Гаусса)

d) Ортоцентры треугольников (BDE), (ABC), (ADF) и (CEF) лежат на одной прямой (прямая Обера)

e) Прямая Гаусса перпендикулярна прямой Обера (теорема Гаусса-Боденмиллера)

https://www.geogebra.org/m/zg4wtmrj

Если вы знаете еще замечательные факты про полный четырехсторонник, будет очень здорово, если вы ими поделитесь @geomweeklyauthor

№18 (Argentinian National Olympiad 1995 level 3)

Внутри параллелограмма ABCD взяли такую точку P, что ∠PDA вдвое меньше ∠ABP и ∠PAD вдвое меньше ∠DCP
Доказать, что AB = BP = CP = CD

№19 (Белорусская математическая олимпиада 2019, 9.6)

Синяя окружность касается медианы треугольника
Доказать, что красная пунктирная окружность касается стороны треугольника

№20 (Вспоминаем точку Фейербаха)

Дан треугольник ABC
O - центр описанной окружности
I - центр вписанной окружности
A_0, B_0, C_0 - точки касания вписанной окружности со сторонами.
A_1, B_1, C_1 - основания биссектрис.
M_A, M_B, M_C - середины сторон.
P - точка на прямой OI, P_A, P_B, P_C - основания перпендикуляров из P на стороны треугольника.
K_B - точка пересечения M_A M_C и A_0 C_0. Аналогично определяются K_A и K_B.
M_AI, M_BI, M_CI - середины AI, BI, CI соответственно

Доказать, что:
a) (M_A M_B M_C) касается (A_0 B_0 C_0) (точка Фейербаха)

b) Точка Фейербаха лежит на прямой B_0 K_B

c) Точка Фейербаха лежит на окружности (A_1, B_1, C_1) (теорема Емельяновых)

d) Точка Фейербаха лежит на окружности (P_A, P_B, P_C) (теорема Фонтене)

e) Точка Фейербаха лежит на окружности (B_0, M_AI, M_CI)

f) Попробуйте сформулировать аналогичные утверждения, но для вневписанной окружности

https://geogebra.org/m/n2ejddyd

№21 (Сборник «Математическое просвещение», третья серия, выпуск 7, 2003)

Доказать, что пунктирные окружности касаются

№22 (Теорема Харта)

Доказать, что существует окружность, касающаяся четырех серых окружностей

№23 (Древний рег)

Доказать, что синие окружности равные тогда и только тогда, когда красные окружности равны

№24 (Осенний тургор 2023, базовый вариант, 10-11.4)

Выбирается случайная точка на окружности, симметричной описанной окружности треугольника относительно стороны. Доказать, что красные отрезки равны

№25 (Отбор на осеннюю тренировочную программу по математике, г. Москва, 2023)

I - инцентр ABC. P - произвольная точка на меньшей дуге AB. W_AW_B || CX. I_1 и I_2 - инцентры APC и PBC.
Доказать, что PI_1I_2Q вписанный

№26 (Осенний тургор 2023, сложный вариант, 10-11.5)

Хорда DE описанной около треугольника ABC окружности пересекает стороны AB и BC в точках P и Q соответственно, точка P лежит между D и Q. В треугольниках ADP и QEC провели биссектрисы DF и EG. Оказалось, что точки D, F, G, E лежат на одной окружности.
Доказать, что точки A, P, Q, C тоже лежат на одной окружности

№27 (ВсОШ ЗЭ 2015, 11.7)

Неравнобедренный треугольник ABC вписан в окружность ω. Касательная к этой окружности в точке А пересекает прямую ВС в точке D. Пусть I — центр окружности, вписанной в треугольник ABC. Прямые BI и CI пересекают биссектрису угла ADB в точках Q и P соответственно. Пусть M — середина отрезка PQ.
Доказать, что прямая MI проходит через
середину дуги ACB окружности ω

№28 (ММО 2023, 11.9)

В треугольнике ABC высоты BE и CF пересекаются в точке H, точка M — середина стороны BC, а X — точка пересечения внутренних касательных к окружностям, вписанным в треугольники BMF и CME.
Доказать, что точки X, M и H лежат на одной прямой

№29 (Обобщение №28)

Доказать, что красные точки лежат на одной прямой

№30 (Источник утерян)

Условие на картинке
Доказать, что красные пунктирные прямые параллельны

№31 (ЮМТ 2019, Гранд-лига, бой за 5-6 тур, задача N5)

На медиане взята произвольная точка
Доказать, что красная пунктирная окружность и красная пунктирная прямая касаются

№32 (ВсОШ ЗЭ 2013, 11.7)

Окружность с центром I, вписанная в треугольник ABC, касается сторон BC, CA, AB в точках A1, B1, C1 соответственно. Пусть Ia, Ib, Ic — центры вневписанных окружностей треугольника ABC, касающихся соответственно сторон BC, CA, AB. Отрезки IaB1 и IbA1 пересекаются в точке C2. Аналогично, отрезки IbC1 и IcB1 пересекаются в точке A2, а отрезки IcA1 и IaC1 — в точке B2. Доказать, что I является центром окружности, описанной около треугольника A2B2C2.

№33 (ВсОШ РЭ 2005, 9.4)

I - инцентр
Доказать, что красные углы равны

№34 (Источник утерян)

Зелные прямые параллельны
Доказать, что красные углы равны

№35 (Шарыгинская олимпиада 2023, 10.6)

Условие на картинке
Доказать, что красные пунктирные прямые пересекаются на окружности