№26 (Осенний тургор 2023, сложный вариант, 10-11.5)
Хорда DE описанной около треугольника ABC окружности пересекает стороны AB и BC в точках P и Q соответственно, точка P лежит между D и Q. В треугольниках ADP и QEC провели биссектрисы DF и EG. Оказалось, что точки D, F, G, E лежат на одной окружности.
Доказать, что точки A, P, Q, C тоже лежат на одной окружности
Хорда DE описанной около треугольника ABC окружности пересекает стороны AB и BC в точках P и Q соответственно, точка P лежит между D и Q. В треугольниках ADP и QEC провели биссектрисы DF и EG. Оказалось, что точки D, F, G, E лежат на одной окружности.
Доказать, что точки A, P, Q, C тоже лежат на одной окружности
❤14💔9✍4
№27 (ВсОШ ЗЭ 2015, 11.7)
Неравнобедренный треугольник ABC вписан в окружность ω. Касательная к этой окружности в точке А пересекает прямую ВС в точке D. Пусть I — центр окружности, вписанной в треугольник ABC. Прямые BI и CI пересекают биссектрису угла ADB в точках Q и P соответственно. Пусть M — середина отрезка PQ.
Доказать, что прямая MI проходит через
середину дуги ACB окружности ω
Неравнобедренный треугольник ABC вписан в окружность ω. Касательная к этой окружности в точке А пересекает прямую ВС в точке D. Пусть I — центр окружности, вписанной в треугольник ABC. Прямые BI и CI пересекают биссектрису угла ADB в точках Q и P соответственно. Пусть M — середина отрезка PQ.
Доказать, что прямая MI проходит через
середину дуги ACB окружности ω
❤8✍8💔1
№32 (ВсОШ ЗЭ 2013, 11.7)
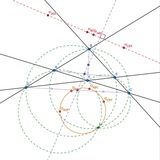
Окружность с центром I, вписанная в треугольник ABC, касается сторон BC, CA, AB в точках A1, B1, C1 соответственно. Пусть Ia, Ib, Ic — центры вневписанных окружностей треугольника ABC, касающихся соответственно сторон BC, CA, AB. Отрезки IaB1 и IbA1 пересекаются в точке C2. Аналогично, отрезки IbC1 и IcB1 пересекаются в точке A2, а отрезки IcA1 и IaC1 — в точке B2. Доказать, что I является центром окружности, описанной около треугольника A2B2C2.
Окружность с центром I, вписанная в треугольник ABC, касается сторон BC, CA, AB в точках A1, B1, C1 соответственно. Пусть Ia, Ib, Ic — центры вневписанных окружностей треугольника ABC, касающихся соответственно сторон BC, CA, AB. Отрезки IaB1 и IbA1 пересекаются в точке C2. Аналогично, отрезки IbC1 и IcB1 пересекаются в точке A2, а отрезки IcA1 и IaC1 — в точке B2. Доказать, что I является центром окружности, описанной около треугольника A2B2C2.
❤12✍7💔3
№37 (Высшая проба 2024, 10.3)
В треугольнике ABC точка I — центр вписанной окружности, E и F — основания биссектрис BI и CI соответственно. Прямая AI пересекает описанную около треугольника EIF окруж- ность в точке T != I. H - ортоцентр треугольника AEF. Доказать, что ортоцентр треугольника AEF равноудален от точек T и I
В треугольнике ABC точка I — центр вписанной окружности, E и F — основания биссектрис BI и CI соответственно. Прямая AI пересекает описанную около треугольника EIF окруж- ность в точке T != I. H - ортоцентр треугольника AEF. Доказать, что ортоцентр треугольника AEF равноудален от точек T и I
❤16💔6✍2
Forwarded from Непрерывное математическое образование
https://geometry.ru/olimp/2024/2024_zaoch_rus_sol.pdf
опубликованы решения заочного тура геометрической олимпиады им. Шарыгина
опубликованы решения заочного тура геометрической олимпиады им. Шарыгина
✍6❤4💔1