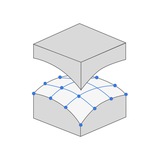
Триангуляция в SOFiSTiK
Когда я публикую посты со своими расчетными моделями, меня периодически спрашивают про странноватый вид конечно-элементной сетки и ее нерегулярность.
Недавно я наткнулся на интересный источник с описанием используемого в SOFiSTiK алгоритма триангуляции. Алгоритм состоит из 3 этапов:
1. Собственно, триангуляция (разбиение пластин на треугольные элементы).
2. Попарная группировка треугольников в четырехугольники. Каждая образованная пара треугольников разделяется на 4 четырехугольника. Не все треугольники найдут себе пару, поэтому некоторые останутся на этом этапе в первоначальном виде.
3. Доработка оставшихся треугольников. Происходит она за счет добавления в центр треугольника узла и деления треугольника на 3 четырехугольника. После этого программа смещает узлы элементов бывшего треугольника, приводя сетку в более качественный вид. Элементы по своей форме становятся ближе к квадратным.
В результате получается сетка, полностью состоящая из четырехузловых элементов, что выглядит очень выигрышно с точки зрения точности получаемых результатов (по сравнению с моделями, содержащими треугольники).
Сама сетка при этом имеет характерный вид, в котором можно увидеть артефакты в виде бывших треугольников, не нашедших себе пары (см. карточку №1).
Когда я публикую посты со своими расчетными моделями, меня периодически спрашивают про странноватый вид конечно-элементной сетки и ее нерегулярность.
Недавно я наткнулся на интересный источник с описанием используемого в SOFiSTiK алгоритма триангуляции. Алгоритм состоит из 3 этапов:
1. Собственно, триангуляция (разбиение пластин на треугольные элементы).
2. Попарная группировка треугольников в четырехугольники. Каждая образованная пара треугольников разделяется на 4 четырехугольника. Не все треугольники найдут себе пару, поэтому некоторые останутся на этом этапе в первоначальном виде.
3. Доработка оставшихся треугольников. Происходит она за счет добавления в центр треугольника узла и деления треугольника на 3 четырехугольника. После этого программа смещает узлы элементов бывшего треугольника, приводя сетку в более качественный вид. Элементы по своей форме становятся ближе к квадратным.
В результате получается сетка, полностью состоящая из четырехузловых элементов, что выглядит очень выигрышно с точки зрения точности получаемых результатов (по сравнению с моделями, содержащими треугольники).
Сама сетка при этом имеет характерный вид, в котором можно увидеть артефакты в виде бывших треугольников, не нашедших себе пары (см. карточку №1).
👍27🔥11👏3😁1💯1
Тут такое дело...зачастил в Москву наведываться этим летом. А посему, разбавлю сине-красно-серую строгость своей ленты эстетичными фотографиями. В архбюро тружусь, как никак!)
🔥40❤15👍9🤩2🤯1
Кто о чем, а он — про балки…
В прошлый раз я закончил на обзоре 6 способов моделирования монолитной балки в составе плиты, и обещал подробнее рассказать о способе с использованием стержневых элементов с тавровым сечением.
Метод моделирования вдохновлен аналитическим подходом к расчету, при котором эффект от совместной работы с плитой учитывается рассмотрением сечения балки как таврового. Подробнее об этом писал вот тут.
У рассматриваемой модели есть 2 недостатка:
1. дублируется собственный вес бетона в пределах эффективной ширины балки
2. дублируется изгибная жесткость плиты в пределах эффективной ширины балки
Первый недостаток идет в запас, поэтому приемлемо. Второй — более неоднозначный. Вот, что написано об этом в книге «Расчет и проектирование конструкций высотных зданий из монолитного железобетона» Городецкого:
Понять этот тезис не так просто. Я попробую объяснить идею с точки зрения моментов инерции.
Элементы плиты и стержень лежат в одной плоскости. А значит, при изгибе между ними не возникает дополнительной пары сил, как в модели с «подвешенным снизу» стержнем.
Момент инерции плиты в пределах эффективной ширины балки — это лишний дубликат. Но так ли он сильно влияет?
В случае нарисованной на карточке балки момент инерции дубликата составляет всего 7,4% от момента инерции тавра. А это значит, что жесткость монолитной балки при моделировании таким способом будет завышена на 7,4%.
Конечно, величина будет меняться в зависимости от геометрии рассматриваемой балки, но главный принцип сохранится — при выравнивании тавра и плиты в одной плоскости, изгибная жесткость дубликата плиты будет заметно меньше, чем у таврового сечения.
В прошлый раз я закончил на обзоре 6 способов моделирования монолитной балки в составе плиты, и обещал подробнее рассказать о способе с использованием стержневых элементов с тавровым сечением.
Метод моделирования вдохновлен аналитическим подходом к расчету, при котором эффект от совместной работы с плитой учитывается рассмотрением сечения балки как таврового. Подробнее об этом писал вот тут.
У рассматриваемой модели есть 2 недостатка:
1. дублируется собственный вес бетона в пределах эффективной ширины балки
2. дублируется изгибная жесткость плиты в пределах эффективной ширины балки
Первый недостаток идет в запас, поэтому приемлемо. Второй — более неоднозначный. Вот, что написано об этом в книге «Расчет и проектирование конструкций высотных зданий из монолитного железобетона» Городецкого:
«Это вполне допустимо, так как конечные элементы плиты моделируют изгибную группу усилий, а часть плиты в составе полки балки — мембранную».
Понять этот тезис не так просто. Я попробую объяснить идею с точки зрения моментов инерции.
Элементы плиты и стержень лежат в одной плоскости. А значит, при изгибе между ними не возникает дополнительной пары сил, как в модели с «подвешенным снизу» стержнем.
Плита и стержень воспринимают внешнюю нагрузку (момент) исключительно за счет своей изгибной жесткости, которая определяется моментом инерции. Проблему можно рассмотреть с точки зрения дублирования момента инерции относительно осей изгиба.
Момент инерции плиты в пределах эффективной ширины балки — это лишний дубликат. Но так ли он сильно влияет?
В случае нарисованной на карточке балки момент инерции дубликата составляет всего 7,4% от момента инерции тавра. А это значит, что жесткость монолитной балки при моделировании таким способом будет завышена на 7,4%.
Конечно, величина будет меняться в зависимости от геометрии рассматриваемой балки, но главный принцип сохранится — при выравнивании тавра и плиты в одной плоскости, изгибная жесткость дубликата плиты будет заметно меньше, чем у таврового сечения.
1🔥25👍15🤯4
Сегодня проводил для ЛШ2024 лекцию, посвященную обзору конструктивных схем и их применению в рамках выполнения архитектурных проектов и макетов.
В выступлении я опирался на классификацию конструктивных систем, описанную в книге «Несущие системы» Энгеля Хайно.
Идея автора в том, чтобы различать системы по механизму их сопротивления внешним силовым воздействиям.
Всего выделяется 4 основополагающих механизма:
1. Адаптация к действующим силам (активные по форме системы)
2. Разложение сил (активные по вектору системы)
3. Сопротивление силам (активные по сечению системы)
4. Рассеивание сил (активные по поверхности системы)
Энгель Хайно преподавал конструкции на архитектурном факультете американского университета. В основу книги легли материалы, которые он готовил и систематизировал для своих студентов.
Я бесконечно уважаю профессионализм и самоотверженность этого человека и всем рекомендую к ознакомлению его произведение!
p.s. книгу в .pdf выложил в комментариях
В выступлении я опирался на классификацию конструктивных систем, описанную в книге «Несущие системы» Энгеля Хайно.
Идея автора в том, чтобы различать системы по механизму их сопротивления внешним силовым воздействиям.
Всего выделяется 4 основополагающих механизма:
1. Адаптация к действующим силам (активные по форме системы)
2. Разложение сил (активные по вектору системы)
3. Сопротивление силам (активные по сечению системы)
4. Рассеивание сил (активные по поверхности системы)
Энгель Хайно преподавал конструкции на архитектурном факультете американского университета. В основу книги легли материалы, которые он готовил и систематизировал для своих студентов.
Я бесконечно уважаю профессионализм и самоотверженность этого человека и всем рекомендую к ознакомлению его произведение!
p.s. книгу в .pdf выложил в комментариях
1👍36🔥14❤8💯1
Моделирование фундамента объемными КЭ
Сейчас на работе встретился интересный случай. Делаю расчетную модель высотного здания. Его фундамент имеет толщину 3 метра при характерных пролетах опирающихся на него конструкций — порядка 6-8 метров.
Если задуматься, такую конструкцию с соотношением толщины к пролету 1:2 было бы неправильно заменять плоской моделью. Такой толщиной просто нельзя пренебрегать, поэтому стоит переходить от плоской модели к объемной.
При стыковке конечных элементов разных размерностей между собой есть нюансы (в моем случае — это объемный фундамент и плоские стены). Если просто соединить их между собой в узлах, то соединение будет работать как шарнирное.
Объясняется это следующим образом. В плоских КЭ, кроме 3-х поступательных степеней свободы узлов (ux, uy, uz) есть еще 3 степени свободы, соответствующие углу поворота узла (φx, φy, φz). За счет последних моделируется изгиб пластин и передается момент.
В объемных КЭ узлы имеют только поступательные степени свободы (ux, uy, uz). Изгиб элемента происходит за счет поступательных смещений узлов.
Чтобы обеспечить жесткое соединение, я завел стены вглубь фундамента на высоту одного КЭ так, чтобы нижние узлы стен совпали с узлами объемных элементов. В таком виде соединение получилось практически абсолютно жестким.
Для моделирования объемной модели я экспортировал обычный плоский фундамент из Revit в SOFiSTiK и далее с помощью CADiNP выдавил плоские элементы фундамента вниз, разбив на 6 слоев с толщиной по 0.5м. Получились 8-узловые объемные КЭ, все узлы которых расположены ровно друг над другом по вертикали. Далее по тому же принципу я выдавил нижние грани стен на 0.5м вниз, таким образом их узлы совпали с узлами объемников. В плане сетка остается нерегулярной.
После однократной настройки алгоритма в CADiNP процесс превращения плоской плиты в объемную получился быстрым и удобным.
Дальше буду анализировать поведение такой модели на упругом полупространстве. Если тема интересна и вам было бы интересно увидеть продолжение — накидайте 🔥!
Сейчас на работе встретился интересный случай. Делаю расчетную модель высотного здания. Его фундамент имеет толщину 3 метра при характерных пролетах опирающихся на него конструкций — порядка 6-8 метров.
Если задуматься, такую конструкцию с соотношением толщины к пролету 1:2 было бы неправильно заменять плоской моделью. Такой толщиной просто нельзя пренебрегать, поэтому стоит переходить от плоской модели к объемной.
При стыковке конечных элементов разных размерностей между собой есть нюансы (в моем случае — это объемный фундамент и плоские стены). Если просто соединить их между собой в узлах, то соединение будет работать как шарнирное.
Объясняется это следующим образом. В плоских КЭ, кроме 3-х поступательных степеней свободы узлов (ux, uy, uz) есть еще 3 степени свободы, соответствующие углу поворота узла (φx, φy, φz). За счет последних моделируется изгиб пластин и передается момент.
В объемных КЭ узлы имеют только поступательные степени свободы (ux, uy, uz). Изгиб элемента происходит за счет поступательных смещений узлов.
Чтобы обеспечить жесткое соединение, я завел стены вглубь фундамента на высоту одного КЭ так, чтобы нижние узлы стен совпали с узлами объемных элементов. В таком виде соединение получилось практически абсолютно жестким.
Для моделирования объемной модели я экспортировал обычный плоский фундамент из Revit в SOFiSTiK и далее с помощью CADiNP выдавил плоские элементы фундамента вниз, разбив на 6 слоев с толщиной по 0.5м. Получились 8-узловые объемные КЭ, все узлы которых расположены ровно друг над другом по вертикали. Далее по тому же принципу я выдавил нижние грани стен на 0.5м вниз, таким образом их узлы совпали с узлами объемников. В плане сетка остается нерегулярной.
После однократной настройки алгоритма в CADiNP процесс превращения плоской плиты в объемную получился быстрым и удобным.
Дальше буду анализировать поведение такой модели на упругом полупространстве. Если тема интересна и вам было бы интересно увидеть продолжение — накидайте 🔥!
3🔥128❤4😱4👏3💯2
В прошлом посте писал о создании расчетной модели толстого плитного фундамента (толщиной 3 м), на которую будет опираться здание высотой около 250 м. Грунты на площадке очень прочные, поэтому без свай.
На текущий момент я выполнил предварительные расчеты на грунтовом основании и сделал первые выводы относительно удобства такой комбинированной модели.
Во-первых, я начал с анализа главных напряжений (растягивающих и сжимающих). Для просмотра напряжений в объемных элементах удобно использовать разрезы. Один из них привел на карточке 2. Картина распределения главных растягивающих и сжимающих напряжений выглядит логично.
Рассеивание сжимающих напряжений от опор вертикальных конструкций вниз происходит по призме, образующие угол около 45 градусов.
Главные растягивающие напряжения концентрируются у опор (у нижней грани плиты) и в пролетах (у верхней грани плиты). Как у перекрытий, только все наоборот.
Во-вторых, армирование в объемных элементах тоже удалось подобрать (карточка 3). Его распределение хорошо коррелирует с траекторией растягивающих напряжений (карточка 4).
Главная сложность — это приведение полученного армирования к привычном виду (плоские изополя для верхней и нижней зоны). Полученные в см2/м2 значения нужно преобразовать в погонную интенсивность в см2/м.
Первая мысль, как это сделать «на коленке» (карточка 5):
1. в нескольких наиболее загруженных сечениях определить среднюю по высоте интенсивность армирования в см2/м2
2. умножив полученное значение на высоту плиты, мы получим значение в см2/м, которое нужно разложить у грани.
Но я понимаю, что это довольно грубое приведение с приличным запасом. Если вы встречали более изящные примеры и методы, — буду благодарен за идеи)
На текущий момент я выполнил предварительные расчеты на грунтовом основании и сделал первые выводы относительно удобства такой комбинированной модели.
Во-первых, я начал с анализа главных напряжений (растягивающих и сжимающих). Для просмотра напряжений в объемных элементах удобно использовать разрезы. Один из них привел на карточке 2. Картина распределения главных растягивающих и сжимающих напряжений выглядит логично.
Рассеивание сжимающих напряжений от опор вертикальных конструкций вниз происходит по призме, образующие угол около 45 градусов.
Главные растягивающие напряжения концентрируются у опор (у нижней грани плиты) и в пролетах (у верхней грани плиты). Как у перекрытий, только все наоборот.
Во-вторых, армирование в объемных элементах тоже удалось подобрать (карточка 3). Его распределение хорошо коррелирует с траекторией растягивающих напряжений (карточка 4).
Главная сложность — это приведение полученного армирования к привычном виду (плоские изополя для верхней и нижней зоны). Полученные в см2/м2 значения нужно преобразовать в погонную интенсивность в см2/м.
Первая мысль, как это сделать «на коленке» (карточка 5):
1. в нескольких наиболее загруженных сечениях определить среднюю по высоте интенсивность армирования в см2/м2
2. умножив полученное значение на высоту плиты, мы получим значение в см2/м, которое нужно разложить у грани.
Но я понимаю, что это довольно грубое приведение с приличным запасом. Если вы встречали более изящные примеры и методы, — буду благодарен за идеи)
Пока вопроса о детальном конструировании плиты не стоит (стадия П), но по полученным результатам я уже считаю, что объемная модель справляется со своей задачей. По крайней мере, фон принять можно. Будущие планы — по полученному результату задаться фоном и проверить его достаточность в режиме физнелина.
1🔥22👍7💯3❤1