Когда все организационные вопросы решены и группа набирается, приятно вернуться к главному — контенту курса.
Сейчас я в самом творческом этапе — проработке презентаций.
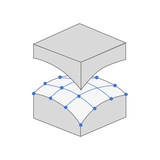
Вчера закончил блок «Как работает метод конечных элементов» — делюсь слайдами, как это получилось!
На курсе мы начнем с погружения в базовые принципы МКЭ и постепенно перейдём к практическим навыкам:
• Построение расчётных моделей — стержневые, оболочковые элементы и их комбинации. Разберём допущения, сеточную сходимость и другие нюансы;
• Понимание разницы линейного и нелинейного подхода, статических и динамических задач — чем они отличаются, и как программа решает их;
• Работа с геометрической и физической нелинейностью — как осознанно применять эти инструменты в инженерных задачах, настраивать параметры и понимать их влияние;
• Критический анализ результатов — как оценить достоверность модели и не попасться на «красивые, но неверные» картинки.
Все темы будут закрепляться практикой: по исходным данным вы будете создавать собственные модели, рассчитывать их в привычной программе, получать обратную связь и разбирать ошибки.
Так формируется настоящий навык выполнения расчетов, который можно использовать в своей практике.
Если вы хотели разобраться в практических нюансах конечно-элементного анализа — сейчас самое время присоединиться:
https://structuralblog.notion.site/
Сейчас я в самом творческом этапе — проработке презентаций.
Вчера закончил блок «Как работает метод конечных элементов» — делюсь слайдами, как это получилось!
На курсе мы начнем с погружения в базовые принципы МКЭ и постепенно перейдём к практическим навыкам:
• Построение расчётных моделей — стержневые, оболочковые элементы и их комбинации. Разберём допущения, сеточную сходимость и другие нюансы;
• Понимание разницы линейного и нелинейного подхода, статических и динамических задач — чем они отличаются, и как программа решает их;
• Работа с геометрической и физической нелинейностью — как осознанно применять эти инструменты в инженерных задачах, настраивать параметры и понимать их влияние;
• Критический анализ результатов — как оценить достоверность модели и не попасться на «красивые, но неверные» картинки.
Все темы будут закрепляться практикой: по исходным данным вы будете создавать собственные модели, рассчитывать их в привычной программе, получать обратную связь и разбирать ошибки.
Так формируется настоящий навык выполнения расчетов, который можно использовать в своей практике.
Если вы хотели разобраться в практических нюансах конечно-элементного анализа — сейчас самое время присоединиться:
https://structuralblog.notion.site/
1👍21🔥13⚡3🤩2
Нужна ли инженеру высшая математика
Вчера в группе канала возник спор о том, насколько важно инженеру знать математику. В частности, прозвучало мнение, что изучая МКЭ-расчеты, надо разбираться и с его математическим аппаратом (а там — линейная алгебра, дифференциальные уравнения и интегралы).
Я уже писал об этом раньше, но, похоже, тема снова стала актуальной. Поделюсь своими мыслями.
Вот у меня в телефоне есть калькулятор. Я не знаю, как он устроен. Кто-то скажет: «Ну тогда удаляй и не пользуйся!» Но я им пользуюсь — и получаю от этого очевидную пользу.
Теперь вернемся к нашей теме. Нужно рассчитать конструкцию и получить достоверные результаты (ее НДС). Для этого у нас есть «калькулятор посложнее» — программа, работающая по методу конечных элементов.
Решение такой задачи обычно включает шесть последовательных этапов:
1. Идеализация — переход от реальной конструкции к расчетной схеме.
2. Дискретизация — переход от расчетной схемы к конечно-элементной модели.
3. Формирование матриц жесткости конечных элементов и сборка глобальной матрицы жесткости системы.
4. Решение системы матричных уравнений равновесия и нахождение узловых перемещений (первичных результатов).
5. Определение вторичных результатов — деформаций, напряжений, внутренних усилий.
6. Анализ результатов: проверка корректности, валидация и верификация.
Вся «математическая соль» МКЭ сосредоточена в этапах 3–5. И именно здесь программы, как правило, не ошибаются — примерно так же, как не ошибается калькулятор, если ввести в него правильное выражение.
Если говорить о практической инженерной задаче, то достоверность расчета определяется тем, насколько корректно выполнены идеализация и дискретизация модели. Это этапы 1–2 — и именно они находятся в зоне ответственности инженера.
Не стоит забывать и про анализ результатов (этап 6). Инженер должен уметь интерпретировать полученные данные — превращать числа и картинки в осмысленные выводы.
А что с математикой? У нее есть свое место и своя роль. Она необходима для теоретических исследований и разработки программных решений. В этих областях без нее действительно не обойтись.
Смешивать эти направления не всегда нужно. Есть теоретики, разработчики и практикующие инженеры — и все они нужны отрасли. Каждый делает свое дело.
Я свой выбор сделал.
Кому со мной по пути — велком на практическое обучение: https://structuralblog.notion.site/
Там не будет разбора фундаментальной математики МКЭ, зато научимся решать практические задачи: выполнять расчеты разнообразных конструкций в линейной и нелинейной постановке.
Вчера в группе канала возник спор о том, насколько важно инженеру знать математику. В частности, прозвучало мнение, что изучая МКЭ-расчеты, надо разбираться и с его математическим аппаратом (а там — линейная алгебра, дифференциальные уравнения и интегралы).
Я уже писал об этом раньше, но, похоже, тема снова стала актуальной. Поделюсь своими мыслями.
Вот у меня в телефоне есть калькулятор. Я не знаю, как он устроен. Кто-то скажет: «Ну тогда удаляй и не пользуйся!» Но я им пользуюсь — и получаю от этого очевидную пользу.
Теперь вернемся к нашей теме. Нужно рассчитать конструкцию и получить достоверные результаты (ее НДС). Для этого у нас есть «калькулятор посложнее» — программа, работающая по методу конечных элементов.
Решение такой задачи обычно включает шесть последовательных этапов:
1. Идеализация — переход от реальной конструкции к расчетной схеме.
2. Дискретизация — переход от расчетной схемы к конечно-элементной модели.
3. Формирование матриц жесткости конечных элементов и сборка глобальной матрицы жесткости системы.
4. Решение системы матричных уравнений равновесия и нахождение узловых перемещений (первичных результатов).
5. Определение вторичных результатов — деформаций, напряжений, внутренних усилий.
6. Анализ результатов: проверка корректности, валидация и верификация.
Вся «математическая соль» МКЭ сосредоточена в этапах 3–5. И именно здесь программы, как правило, не ошибаются — примерно так же, как не ошибается калькулятор, если ввести в него правильное выражение.
Если говорить о практической инженерной задаче, то достоверность расчета определяется тем, насколько корректно выполнены идеализация и дискретизация модели. Это этапы 1–2 — и именно они находятся в зоне ответственности инженера.
Не стоит забывать и про анализ результатов (этап 6). Инженер должен уметь интерпретировать полученные данные — превращать числа и картинки в осмысленные выводы.
На этом основано мое понимание того, как изучать расчеты с точки зрения их практического применения. Фокус — на подготовке корректных входных данных и на осмысленное понимание результатов.
А что с математикой? У нее есть свое место и своя роль. Она необходима для теоретических исследований и разработки программных решений. В этих областях без нее действительно не обойтись.
Смешивать эти направления не всегда нужно. Есть теоретики, разработчики и практикующие инженеры — и все они нужны отрасли. Каждый делает свое дело.
Начинающему специалисту важно понять, что ему ближе, и развиваться в выбранном направлении. Все и сразу — обычно не получается.
Я свой выбор сделал.
Кому со мной по пути — велком на практическое обучение: https://structuralblog.notion.site/
Там не будет разбора фундаментальной математики МКЭ, зато научимся решать практические задачи: выполнять расчеты разнообразных конструкций в линейной и нелинейной постановке.
1🔥32❤16👏10👍5⚡1
Задача на инженерную интуицию
Здание Commerzbank Tower было построено в 1997 (Франкфурт-на-Майне, Германия) по проекту студии Нормана Фостера. Несущая система треугольной в плане башни состоит из 3 ядер жесткости, соединенных между собой безраскосными стальными фермами, часто называемыми фермами Виренделя.
Главная особенность таких ферм — отсутствие диагональных раскосов. Восприятие нагрузок происходит за счет включения всех ее элементов в изгибные деформации. По сути, это рама.
Основной критерий, определяющий облик и габариты таких ферм, поддерживающих целые этажи — их жесткость. И поэтому главная задача их расчета — точная оценка их перемещений под действующими вертикальными нагрузками.
Рассмотрим подходы к решению этой задачи на простом примере. Есть ферма Виренделя, состоящая из 4 панелей. Узлы — жесткие, усиленные косынками. Для этой конструкции можно придумать по крайней мере 2 расчетные КЭ-модели:
Модель №1 — самая простая стержневая.
Модель №2 — более детализированная, с использованием пластинчатых элементов.
Нагрузки, условия закрепления моделей идентичны. Главное отличие — в размерности используемых конечных элементов и соответствующей детализации.
Как думаете, насколько максимальное перемещение Δ двух моделей будет отличаться и почему оно вообще должно отличаться? Варианты объяснений пишите в комментарии, а прогноз — в голосовании ниже:)
Здание Commerzbank Tower было построено в 1997 (Франкфурт-на-Майне, Германия) по проекту студии Нормана Фостера. Несущая система треугольной в плане башни состоит из 3 ядер жесткости, соединенных между собой безраскосными стальными фермами, часто называемыми фермами Виренделя.
Главная особенность таких ферм — отсутствие диагональных раскосов. Восприятие нагрузок происходит за счет включения всех ее элементов в изгибные деформации. По сути, это рама.
Основной критерий, определяющий облик и габариты таких ферм, поддерживающих целые этажи — их жесткость. И поэтому главная задача их расчета — точная оценка их перемещений под действующими вертикальными нагрузками.
Рассмотрим подходы к решению этой задачи на простом примере. Есть ферма Виренделя, состоящая из 4 панелей. Узлы — жесткие, усиленные косынками. Для этой конструкции можно придумать по крайней мере 2 расчетные КЭ-модели:
Модель №1 — самая простая стержневая.
Модель №2 — более детализированная, с использованием пластинчатых элементов.
Нагрузки, условия закрепления моделей идентичны. Главное отличие — в размерности используемых конечных элементов и соответствующей детализации.
Как думаете, насколько максимальное перемещение Δ двух моделей будет отличаться и почему оно вообще должно отличаться? Варианты объяснений пишите в комментарии, а прогноз — в голосовании ниже:)
1🔥11👍4💯4❤2⚡1
Насколько будет отличаться максимальное перемещение Δ в двух КЭ-моделях безраскосной фермы?
Anonymous Quiz
28%
≈15%
31%
≈30%
9%
≈50%
5%
≈70%
27%
без понятия, посмотреть результаты
🔥7😱1
Разбор задачи — МКЭ-модель безраскосной фермы
В голосовании выше мы имеем всего 5% правильных ответов. Это значит, что автору удалось-таки удивить (или запутать) свою аудиторию. Надеюсь, больше первое.
Как уже многие догадались, дьявол кроется в узлах. Конкретно — в их больших габаритах и относительно большой жесткости по сравнению с гибкой частью ригелей и стоек.
Для наглядного анализа этой задачи я подготовил и сравнил 6 расчетных моделей. Их описание и результаты показаны на карточках.
На что хочется обратить внимание:
1. Модель из пластин — эталонная. На этом подробно останавливаться не буду.
2. Эквивалентность условий закрепления моделей — за этим нужно следить. В них часто кроются причины расхождения между стержневыми моделями и моделями из пластин.
3. Сеточная сходимость: особенно важно для моделей из пластин. Особенно, если пластины работают на изгиб в своей плоскости (привет, сдвиговое запирание)
4. Чувствительность к нелинейным эффектам. Расчет произведен в линейной постановке. Это обосновано тем, что при рассматриваемой нагрузке все работает в упругой стадии (эквивалентные напряжения показаны на последней карточке). Влияния эффектов геометрической жесткости тут тоже не предвидится.
Призом личных симпатий хочется отметить модель №3 (расхождение с эталоном 7%). Такой прием локальной детализации узла часто используется на больших схемах. Это позволяет, с одной стороны, корректно учесть жесткость узла и найти его НДС, с другой — не утяжелять всю модель. При этом нужно следить за корректностью стыковки фрагмента со смежными элементами. Для этого концевой узел стержня соединен с торцом узла жесткой вставкой. Это позволяет соблюсти гипотезу плоских сечений на границе узел-стержень.
Модель №5, признанная мною как удачная (расхождение с эталоном 12%), родилась на интуиции. Потому что довольно очевидно, что в модели 4 жесткость узла занижена, а в 6 — завышена.
На разборе подобных задач построена практическая часть моего нового курса КЭ-модели СК.
Через решение и разбор разнообразных кейсов, подобных этому, мы изучаем различные аспекты МКЭ-моделирования. И все это не знания в вакууме — а то, что нужно применять в ежедневной практике, если вы занимаетесь расчетами или хотите ими заниматься по мере профессионального роста.
Буду рад видеть каждого из вас на первом и единственном офлайн-потоке проекта — места еще остались. Переходите на сайт, там собрана вся подробная информация — занимайте свое место, и мы начнем наше совместное развитие уже в следующее воскресенье!
В голосовании выше мы имеем всего 5% правильных ответов. Это значит, что автору удалось-таки удивить (или запутать) свою аудиторию. Надеюсь, больше первое.
Как уже многие догадались, дьявол кроется в узлах. Конкретно — в их больших габаритах и относительно большой жесткости по сравнению с гибкой частью ригелей и стоек.
Для наглядного анализа этой задачи я подготовил и сравнил 6 расчетных моделей. Их описание и результаты показаны на карточках.
На что хочется обратить внимание:
1. Модель из пластин — эталонная. На этом подробно останавливаться не буду.
2. Эквивалентность условий закрепления моделей — за этим нужно следить. В них часто кроются причины расхождения между стержневыми моделями и моделями из пластин.
3. Сеточная сходимость: особенно важно для моделей из пластин. Особенно, если пластины работают на изгиб в своей плоскости (привет, сдвиговое запирание)
4. Чувствительность к нелинейным эффектам. Расчет произведен в линейной постановке. Это обосновано тем, что при рассматриваемой нагрузке все работает в упругой стадии (эквивалентные напряжения показаны на последней карточке). Влияния эффектов геометрической жесткости тут тоже не предвидится.
Призом личных симпатий хочется отметить модель №3 (расхождение с эталоном 7%). Такой прием локальной детализации узла часто используется на больших схемах. Это позволяет, с одной стороны, корректно учесть жесткость узла и найти его НДС, с другой — не утяжелять всю модель. При этом нужно следить за корректностью стыковки фрагмента со смежными элементами. Для этого концевой узел стержня соединен с торцом узла жесткой вставкой. Это позволяет соблюсти гипотезу плоских сечений на границе узел-стержень.
Модель №5, признанная мною как удачная (расхождение с эталоном 12%), родилась на интуиции. Потому что довольно очевидно, что в модели 4 жесткость узла занижена, а в 6 — завышена.
На разборе подобных задач построена практическая часть моего нового курса КЭ-модели СК.
Через решение и разбор разнообразных кейсов, подобных этому, мы изучаем различные аспекты МКЭ-моделирования. И все это не знания в вакууме — а то, что нужно применять в ежедневной практике, если вы занимаетесь расчетами или хотите ими заниматься по мере профессионального роста.
Буду рад видеть каждого из вас на первом и единственном офлайн-потоке проекта — места еще остались. Переходите на сайт, там собрана вся подробная информация — занимайте свое место, и мы начнем наше совместное развитие уже в следующее воскресенье!
1👍17❤9🔥8