Вот такой есть факт от @Mamonovclhgffkuffhj.
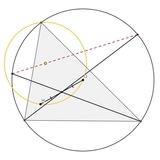
Х125 - центр гиперболы Джерабека, а красная точка на рисунке - его изотомическое + изогональное сопряжение. Фокусы эллипса на рисунке - О и Н; доказать касание.
Интересно, может ли это кто-то решить геометрически?
Х125 - центр гиперболы Джерабека, а красная точка на рисунке - его изотомическое + изогональное сопряжение. Фокусы эллипса на рисунке - О и Н; доказать касание.
Интересно, может ли это кто-то решить геометрически?
🤮8❤2🐳2👍1🤡1
Добрый день, сегодня задача моего авторства (она отстояла в очереди по честному).
Условие:
Определим S - треугольник точки Р относительно треугольника АВС как на первом рисунке (синий - это S-треуг.)
Построим всевозможные S-треугольники на картинке с АВС и Н (ортоцентром), тогда центроиды таких S-треугольников образуют ортоцентрическую четверку.
Условие:
Определим S - треугольник точки Р относительно треугольника АВС как на первом рисунке (синий - это S-треуг.)
Построим всевозможные S-треугольники на картинке с АВС и Н (ортоцентром), тогда центроиды таких S-треугольников образуют ортоцентрическую четверку.
🤡9🔥4✍2👍2❤1🤯1💊1
Что ж, будем пытаться чередовать добрые и недобрые задачи... Сегодня факт от @Mamonovclhgffkuffhj про ту же конструкцию, что и позапрошлый пост.
Оказывается, три эллипса на рисунке имеют общую касательную (красный - эллипс Штейнера). Оказывается, что она проходит через центр гиперболы Киперта и его изотомическое + изогональное сопряжение.
Оказывается, три эллипса на рисунке имеют общую касательную (красный - эллипс Штейнера). Оказывается, что она проходит через центр гиперболы Киперта и его изотомическое + изогональное сопряжение.
🔥3❤2🤡2👍1
Вот довольно олимпиадная задача от меня. Она была в серии из авторок кружковцев МатЦентра, а на днях появилась в какой-то ЦПМовской серии; поэтому я не вижу проблем, чтобы опубликовать ее здесь.
Во вписанном четырёхугольнике ABCD точки Лемуана треугольников ABC, BCD, CDA, DAB лежат на одной окружности. Доказать, что ABCD - трапеция.
На самом деле, это же верно и для точек Жергонна, Нагеля и других; но доказательство уже перестает быть добрым.
Во вписанном четырёхугольнике ABCD точки Лемуана треугольников ABC, BCD, CDA, DAB лежат на одной окружности. Доказать, что ABCD - трапеция.
На самом деле, это же верно и для точек Жергонна, Нагеля и других; но доказательство уже перестает быть добрым.
❤3👍2🤡2🔥1
Снова факт от нашего основного спонсора недобрых задач @Mamonovclhgffkuffhj.
На картинке Why-pointы отразили относительно сторон треугольника; доказать касание.
Upd: https://news.1rj.ru/str/olympgeom/1265 - определение Why-pointов.
Х_99 - перспектор параболы Киперта.
На картинке Why-pointы отразили относительно сторон треугольника; доказать касание.
Upd: https://news.1rj.ru/str/olympgeom/1265 - определение Why-pointов.
Х_99 - перспектор параболы Киперта.
❤4👍1🔥1🤡1
Надо ли писать определения точек и объектов, которые есть в задачах, а также давать ссылки на материалы, где про это можно почитать?
Anonymous Poll
92%
Да
8%
Нет
🤡1
Встречайте задачу от @don_schijuan... Первую в канале, для которой нужно аж две картинки 💥!
На ОБЕИХ картинках маленькие синие точки - середины дуг описанной окружности и точки касания вписанной окружности. Na' - точка, изогонально сопряжённая точке Нагеля АВС. Оказывается, что красная прямая одна и та же.
Upd: про точку, изогонально сопряженную Na (X_56), можно почитать здесь: https://faculty.evansville.edu/ck6/encyclopedia/ETC.html.
А красная прямая из задачи проходит через точкуХ_222 , которая является рад.центром трех аналогичных окружностей, две из которых нарисованы на первой картинке. К сожалению, в источнике выше (про иксы) информации о ней довольно мало.
На ОБЕИХ картинках маленькие синие точки - середины дуг описанной окружности и точки касания вписанной окружности. Na' - точка, изогонально сопряжённая точке Нагеля АВС. Оказывается, что красная прямая одна и та же.
Upd: про точку, изогонально сопряженную Na (X_56), можно почитать здесь: https://faculty.evansville.edu/ck6/encyclopedia/ETC.html.
А красная прямая из задачи проходит через точку
❤5🔥5🤯1🤡1
Geometry Daily
Надо ли писать определения точек и объектов, которые есть в задачах, а также давать ссылки на материалы, где про это можно почитать?
Что ж, походу, почти единогласно...
❤4
animation.gif
10.2 MB
Первая анимация в канале 🤯 ! За задачу спасибо @vkomplahposchitaetsa
Udp: точка снизу - середина дуги. Выделенных четырёхугольник вписанно-описанный.
Udp: точка снизу - середина дуги. Выделенных четырёхугольник вписанно-описанный.
Please open Telegram to view this post
VIEW IN TELEGRAM
❤10👍4👏2🔥1
Задача от @emil_sadykov.
ХУZ - правильный треугольник, описанная окружность около которого концентрична с (АВС) и имеет радиус в √2 раз больше. Х', У', Z' - изогональные сопряжения Х, У, Z. Доказать, что центр масс Х'У'Z' - это Х_20 АВС.
Upd: Х_20 - отражение ортоцентра треугольника относительно центра описанной окружности.
ХУZ - правильный треугольник, описанная окружность около которого концентрична с (АВС) и имеет радиус в √2 раз больше. Х', У', Z' - изогональные сопряжения Х, У, Z. Доказать, что центр масс Х'У'Z' - это Х_20 АВС.
Upd: Х_20 - отражение ортоцентра треугольника относительно центра описанной окружности.
✍5👍4🔥1
Задача от @Edinburgh_of_the_Seven_Seas
Докажите, что если центр синей коники лежит на красной прямой, то он лежит и на пунктирной прямой.
Докажите, что если центр синей коники лежит на красной прямой, то он лежит и на пунктирной прямой.
🤡12🔥9👍2👏1
Надеюсь, что все уже успели насладиться задачами из SL IMO.
Теперь мы продолжаем выкладывать ваши задачи. Сегодня вот такая красота от @Mamonovclhgffkuffhj.
Upd: Fe - точка Фейербаха АВС, I - инцентр АВС, O - центр описанной окружности АВС, синяя точка - проекция ортоцентра АВС на прямую OI.
Теперь мы продолжаем выкладывать ваши задачи. Сегодня вот такая красота от @Mamonovclhgffkuffhj.
Upd: Fe - точка Фейербаха АВС, I - инцентр АВС, O - центр описанной окружности АВС, синяя точка - проекция ортоцентра АВС на прямую OI.
Добрый вечер!
Разминочная задачка от меня.
Докажите, что центроиды черного и фиолетового треугольников совпадают.
(то, что под спойлером не относится к решению)
если что, у нас еще очень много задач в отложке, просто большинство из них - недобрые факты от @Mamonovclhgffkuffhj ).
Вот мы и решили дать какую то разминочную доброту 😀
Разминочная задачка от меня.
Докажите, что центроиды черного и фиолетового треугольников совпадают.
(то, что под спойлером не относится к решению)
Вот мы и решили дать какую то разминочную доброту
Please open Telegram to view this post
VIEW IN TELEGRAM
❤6👍2🔥2
Forwarded from Geomega
Обобщение окружности Конвея. Не мог не сделать пост про это, уж больно красиво конструкция выглядит, как по мне
Сегодня пост с красивой задачей от @egfed.
L - отражение ортоцентра АВС относительно центра описанной окружности, L' - изогональное сопряжение L. Доказать вписанность...
L - отражение ортоцентра АВС относительно центра описанной окружности, L' - изогональное сопряжение L. Доказать вписанность...
❤10🔥5👎3
Красивая задача про треугольник с углом 60° от @Edinburgh_of_the_Seven_Seas.
Собственно, центры цветных окружностей - середины хорд (АВС), содержащих биссектрисы; и они касаются соотв. сторон треугольника. Доказать, что цветные окружности также касаются прямой, проходящей через середину М АС (и перп. МХ_125, но это условие можно игнорировать).
Собственно, центры цветных окружностей - середины хорд (АВС), содержащих биссектрисы; и они касаются соотв. сторон треугольника. Доказать, что цветные окружности также касаются прямой, проходящей через середину М АС (
🤯9🔥6🤡2😍2
Geometry Daily
Народная задача от @Edinburgh_of_the_Seven_Seas Красиво 🤤
Это дополнение к этой задаче...
😱7🔥3👏2