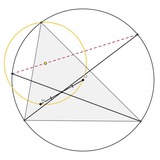
Народная задача.
Теперь шиза от @SaikenQA.
Синие точки на рисунке - середины больших дуг.
Доказать, что пунктирные прямые пересекаются на окружности.
Теперь шиза от @SaikenQA.
Синие точки на рисунке - середины больших дуг.
Доказать, что пунктирные прямые пересекаются на окружности.
🤮7❤🔥3
Вечерняя разминка №6
Инструмент "Разделитель" может выполнять только два типа операций:
1) Для трёх точек Х, У, Z проводить внутреннюю биссектрису угла XYZ.
2) Отмечать точку пересечения проведенных прямых.
Как при помощи "Разделителя" отметить центр окружности, описанной около треугольника АВС (А, В, С отмечены)?
Инструмент "Разделитель" может выполнять только два типа операций:
1) Для трёх точек Х, У, Z проводить внутреннюю биссектрису угла XYZ.
2) Отмечать точку пересечения проведенных прямых.
Как при помощи "Разделителя" отметить центр окружности, описанной около треугольника АВС (А, В, С отмечены)?
🍓2
Задача от одного из админов с "Формулы единства" этого года.
Пусть A_1, B_1, C_1 середины сторон треугольника ABC, a точки касания вписанной - A_2, B_2, C_2. Пусть x - количество точек пересечения B_2C_2 и вписанной окружности AB_1C_1. y и z определены аналогично. Найдите максимальное значение x+y+z.
Видимо, разминка №7
Пусть A_1, B_1, C_1 середины сторон треугольника ABC, a точки касания вписанной - A_2, B_2, C_2. Пусть x - количество точек пересечения B_2C_2 и вписанной окружности AB_1C_1. y и z определены аналогично. Найдите максимальное значение x+y+z.
Видимо, разминка №7
🤮16💩7❤3
Народная задача!
Автор - Иван Часовских (@IvanMChas)
РЕШАТЬ ЭТО НИКТО В МИРЕ НЕ УМЕЕТ, ВЫ МОЖЕТЕ СТАТЬ ПЕРВЫМ!
(Ба A-точка Болтая ABC, Бab Бa-точка Болтая ABБa и т.д.)
Доказать подобие желтых треугольников.
Автор - Иван Часовских (@IvanMChas)
РЕШАТЬ ЭТО НИКТО В МИРЕ НЕ УМЕЕТ, ВЫ МОЖЕТЕ СТАТЬ ПЕРВЫМ!
(Ба A-точка Болтая ABC, Бab Бa-точка Болтая ABБa и т.д.)
Доказать подобие желтых треугольников.
👎6👍5🔥4🏆2
Вечерняя разминка №8
Клетчатый квадрат (2N + 1)(2N + 1) разбили на треугольники с вершинами в узлах клеток. Доказать, что среди треугольников разбиения есть тот, площадь которого нецелая.
Клетчатый квадрат (2N + 1)(2N + 1) разбили на треугольники с вершинами в узлах клеток. Доказать, что среди треугольников разбиения есть тот, площадь которого нецелая.
❤8
Народная и очень красивая задача!
Авторы - @vkomplahposchitaetsa и @rslrg111
Красная точка - середина отрезка (на котором она лежит).
Авторы - @vkomplahposchitaetsa и @rslrg111
Красная точка - середина отрезка (на котором она лежит).
🔥10
ну и на вечер у нас ваша любимая СТЕРЕОМЕТРИЯ.
Хорды АА', ВВ', СС' сферы пересекаются в точке О. Доказать, что плоскости АВС и А'В'С' отсекают от хорды ХХ', проходящей через О, равные отрезки тогда и только тогда, когда О - середина ХХ'.
Разминка №11.
Хорды АА', ВВ', СС' сферы пересекаются в точке О. Доказать, что плоскости АВС и А'В'С' отсекают от хорды ХХ', проходящей через О, равные отрезки тогда и только тогда, когда О - середина ХХ'.
Разминка №11.
🤮12💩3🤡3
Разминка №12
В треугольнике ABC центр описанной окружности отразили относительно сторон AC, AB и получили соответственно точки E, F. Пусть M и N (красные точки на рисунке) - центры окружностей (OBE) и (OCF), а K и L (чёрные точки на рисунке) - ортоцентры треугольников ABE и ACF (красных треугольников на рисунке).
Доказать, что MN || KL.
В треугольнике ABC центр описанной окружности отразили относительно сторон AC, AB и получили соответственно точки E, F. Пусть M и N (красные точки на рисунке) - центры окружностей (OBE) и (OCF), а K и L (чёрные точки на рисунке) - ортоцентры треугольников ABE и ACF (красных треугольников на рисунке).
Доказать, что MN || KL.
❤1👍1
Народная задача.
Автор - @timofeyxd
Сиреневые точки на рисунке диаметрально противоположны на красной окружности.
Автор - @timofeyxd
Сиреневые точки на рисунке диаметрально противоположны на красной окружности.
🔥3
Ну и на вечер снова СТЕРЕОМЕТРИЯ ахаха
Тетраэдр АBCD с остроугольными гранями вписан в сферу с центром в точке О. Прямая DO пересекает ее второй раз в точке D', а плоскость АВС - в точке P. Доказать, что если угол APB вдвое больше угла АСВ, то углы АDD', BDD' равны.
Разминка №13.
Тетраэдр АBCD с остроугольными гранями вписан в сферу с центром в точке О. Прямая DO пересекает ее второй раз в точке D', а плоскость АВС - в точке P. Доказать, что если угол APB вдвое больше угла АСВ, то углы АDD', BDD' равны.
Разминка №13.
❤5🤮2💩2🤡2
Пусть ABC - правильный треугольник. На его сторонах выбраны точки S и R. Точка R - центр окружности (KXL), а точка S - центр окружности (CXK); CK = AL = AB. Точки P, Q на отрезках SC, AR - произвольные. На отрезке SX отложили точку P1 так, что SP1 = SP, на отрезке RX отложили точку Q1 так, что RQ1 = RQ. Докажите, наконец, что из отрезков KP, LQ, P1Q1 можно составить треугольник.
Разминка №14.
Разминка №14.
❤3🤡1
Народная задача!
Автор - величайший @euclid_is_dead.
Условие: Есть вписанный четырёхугольник ABCD и окружность w, касающаяся прямых AB и CD. Через A и B проведена окружность w1, касающаяся w. Через C и D проведена окружность w2, касающаяся w. Пусть l-общая внешняя касательная w1 и w2. Доказать, что существует парабола, проходящая через A, B, C, D и касающаяся l.
Автор - величайший @euclid_is_dead.
Условие: Есть вписанный четырёхугольник ABCD и окружность w, касающаяся прямых AB и CD. Через A и B проведена окружность w1, касающаяся w. Через C и D проведена окружность w2, касающаяся w. Пусть l-общая внешняя касательная w1 и w2. Доказать, что существует парабола, проходящая через A, B, C, D и касающаяся l.