№47 (IMO 2024, 4)
Пусть ABC – треугольник, в котором AB < AC < BC. Пусть ω – вписанная в треугольник ABC окружность, а I – ее центр. Пусть X – такая точка на прямой BC, отличная от C, что прямая, проходящая через X параллельно AC, касается ω. Аналогично, пусть Y – такая точка на прямой BC, отличная от B, что прямая, проходящая через Y параллельно AB, касается ω. Пусть AI пересекает описанную около треугольника ABC окружность второй раз в точке P != A. Пусть K и L – середины сторон AB и AC соответственно. Доказать, что ∠KIL + ∠YPX = 180◦
Пусть ABC – треугольник, в котором AB < AC < BC. Пусть ω – вписанная в треугольник ABC окружность, а I – ее центр. Пусть X – такая точка на прямой BC, отличная от C, что прямая, проходящая через X параллельно AC, касается ω. Аналогично, пусть Y – такая точка на прямой BC, отличная от B, что прямая, проходящая через Y параллельно AB, касается ω. Пусть AI пересекает описанную около треугольника ABC окружность второй раз в точке P != A. Пусть K и L – середины сторон AB и AC соответственно. Доказать, что ∠KIL + ∠YPX = 180◦
❤9✍1
Geometry Weekly
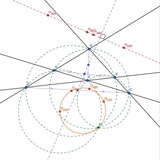
№48 (Сюжетик) Фиолетовые окружности касаются двух сторон треугольника и его окружности девяти точек. Доказать, что их центры на одной прямой
№49 (И небольшой спойлер-усиление к предыдущей задаче)
H - ортоцентр, Be - точка Бевэна ( https://en.wikipedia.org/wiki/Bevan_point ). Вообще, можно обойтись и без Be
❤8✍4
Forwarded from Олимпиадная геометрия
Много геометрических каналов, конечно, развелось... проще перечислить тех, у кого их нет... но я попробую в почти случайном порядке перечислить те, что есть.
Геометрия-канал старейший геометрический канал
Geometry Ukraine
Geometry Belarus
геометрия от Волчкевича
геометрия с Федором Ниловым
NeuroGeometry геометрия с не только лишь человеческим лицом
канал Ярослава Щербатова специалиста по Акопяну
канал Задача дня Юсуфа Нагуманова
Geometry Weekly автор скрывает свое имя... но мы то знаем...
У многих каналов есть свои чаты, но их уж я упоминать не буду. Наверняка, есть еще десяток, можете скинуть в комментариях, если действительно туда стоит заходить...
Геометрия-канал старейший геометрический канал
Geometry Ukraine
Geometry Belarus
геометрия от Волчкевича
геометрия с Федором Ниловым
NeuroGeometry геометрия с не только лишь человеческим лицом
канал Ярослава Щербатова специалиста по Акопяну
канал Задача дня Юсуфа Нагуманова
Geometry Weekly автор скрывает свое имя... но мы то знаем...
У многих каналов есть свои чаты, но их уж я упоминать не буду. Наверняка, есть еще десяток, можете скинуть в комментариях, если действительно туда стоит заходить...
❤12
№55 (Комбигеома)
Для каких n в пространстве размерности n существуют 2^n попарно параллельных гиперплоскостей, таких, что между соседними гиперплоскостями расстояния равны и на каждой из них можно взять по точке так, чтобы точки образовывали гиперкуб?
Для каких n в пространстве размерности n существуют 2^n попарно параллельных гиперплоскостей, таких, что между соседними гиперплоскостями расстояния равны и на каждой из них можно взять по точке так, чтобы точки образовывали гиперкуб?
✍7❤4💔4
№60 (ВсОШ РЭ 2025, 11.5)
Треугольник ABC вписан в окружность Ω. Пусть прямые AD, BE и CF - его высоты, а точки M, N и P - середины сторон BC, AC и AB соответственно. Прямые AM, BN и CP пересекают описанную окружность треугольника DEF в точках I, J и K соответственно. Описанные окружности треугольников AID, BJE и CKF пересекают Ω в точках X, Y и Z, соответственно. Точки А', B' и C' - отражения точек X, Y, Z соответственно относительно M, N и P соответственно.
Доказать, что прямые AA', BB', CC' пересекаются в одной точке
Треугольник ABC вписан в окружность Ω. Пусть прямые AD, BE и CF - его высоты, а точки M, N и P - середины сторон BC, AC и AB соответственно. Прямые AM, BN и CP пересекают описанную окружность треугольника DEF в точках I, J и K соответственно. Описанные окружности треугольников AID, BJE и CKF пересекают Ω в точках X, Y и Z, соответственно. Точки А', B' и C' - отражения точек X, Y, Z соответственно относительно M, N и P соответственно.
Доказать, что прямые AA', BB', CC' пересекаются в одной точке
💔24❤21
№61 (SteelBrawl Shop)
Дан остроугольный треугольник ABC. Высоты, проведенные из точек A и B, пересекаются в точке H и пересекают внешнюю биссектрису угла C в точках Y и X соответственно. Внешняя биссектриса угла AHB пересекает отрезки AX и BY в точках P и Q соответственно.
Доказать, что если PX = QY, то
AP + BQ >= 2CH.
Дан остроугольный треугольник ABC. Высоты, проведенные из точек A и B, пересекаются в точке H и пересекают внешнюю биссектрису угла C в точках Y и X соответственно. Внешняя биссектриса угла AHB пересекает отрезки AX и BY в точках P и Q соответственно.
Доказать, что если PX = QY, то
AP + BQ >= 2CH.
❤14✍1👍1💔1
Милая полуночная задачка. Авторство приписывают легендарному TelvCohl-ю.
И вдогонку пара интересных вопросов:
а) Пусть красный вектор фиксирован. Как построить чертёж к задаче в геогебре?
б) Можно ли обойтись циркулем и линейкой?
Соответствующие пары точек изогонально сопряжены в треугольнике ABC, красные векторы равны. Докажите, что P — ортоцентр треугольника P_1P_2P_3.
И вдогонку пара интересных вопросов:
а) Пусть красный вектор фиксирован. Как построить чертёж к задаче в геогебре?
б) Можно ли обойтись циркулем и линейкой?
❤9
Forwarded from Geometry Daily
Теперь хочу анонсировать главную идею канала - это канал народа, созданный для народа, в котором будут публиковаться ЗАДАЧИ ОТ НАРОДА! Если вы хотите, чтобы ваша задача(не обязательно авторка, просто красивая, не очень известная задача) появилась в этом канале, то просто киньте ее мне @OttoLFS ! Это конечно может быть и авторка, которую не взяли на олимпиаду, или которая просто выглядит как шиза про 10 точек болтая(условно). Все задачи приветствуется, и будут обработаны. 👍 👍 👍 👍 👍
Please open Telegram to view this post
VIEW IN TELEGRAM
❤🔥10😢1